Lista 1A

Os exercícios abordados na atividade 1 estão relacionados com a aritmética do ponto flutuante: erros absolutos e relativos; Arredondamento e truncamento.

Aritmética do ponto flutuante começou a ser adotada quando um grupo de engenheiros de diferentes empresas de computação encontrou um padrão de representação dos números que deveria ser usado na construção de computadores. A base numérica do computador é binária e são adotados dois formatos para a representação dos números: Precisão simples e precisão dupla. Por precisão simples, um número seria representado por 32 bits, sendo 1 bit reservado para o sinal do número, 8 bits para o expoente da base e 23 bits reservados para a mantissa. O sistema de precisão dupla é mais utilizado quando é preciso usar números muito pequenos ou muito grandes pois há maior precisão para a mantissa e para intervalos maiores para o expoente; nele há 64 bits, sendo 1 bit para o sinal, 11 bits para o expoente da base e 52 bits para a mantissa.

Frequentemente a aritmética entre dois números na representação de ponto flutuante não é exata, isso é devido a maneira como esses dois números são somados, pois nesse procedimento, dois algarismos menos significativos do menor operando são descartados, o que pode resultar em uma soma não exata. Esse tipo de erro é chamado de erro de arredondamento.

O erro de truncamento ocorre porque muitos métodos computam aproximações discretas para uma quantidade contínua desejada; devido ao truncamento e ao arredondamento, erros de precisão acontecem, levando a um erro absoluto, que compara o resultado obtido com o que era esperado, e consequentemente a um erro relativo.

Atividade 1

Mostre qual é o maior e o menor número ﬂutuante que seu computador trabalha, realmax e realmin no MatLab. Mostre qual é o epsilon de sua máquina, eps no MatLab. O que quer dizer cada um destes valores?

O programa utilizado foi o Scilab, semelhante ao matlab.

Os comandos realmax e realmin do matlab são equivalentes aos comandos number_properties("huge") e number_properties("tiny") no scilab, respectivamente.

Dessa maneira, ao digitar esses comandos no scilab, os resultados obtidos foram:

Execução de iniciação:

carregando o ambiente inicial

-->number_properties("huge") //Comando para mostrar qual o maior número flutuante

ans =

1.79D+308

-->number_properties("tiny") //Comando para mostrar qual o menor número flutuante

ans =

2.22D-308

Ponto flutuante é a forma de representação de um número real no computador. O maior número flutuante será o maior número que a máquina utilizada pode reproduzir, no caso do exemplo anterior, esse número é 1.79 e+308. Já o menor número flutuante, no exemplo, 2.22 e-308, é o menor número representado pelo computador utilizado.

Já o comando eps no Matlab é equivalente à %eps no scilab. Portanto o épsilon da máquina é:

Execução de iniciação:

carregando o ambiente inicial

-->%eps //Comando para descobrir o épsilon da máquina

%eps =

2.220D-16

O épsilon significa a menor distância relativa entre dois números, indicando a precisão da maquina utilizada. Portanto o resultado acima afirma que 2.220D-16 é essa menor distância relativa e que 1+ 2.220D-16 é diferente de 1, mas 1+[( 2.220D-16)/3] é igual a 1 pois [( 2.220D-16)/3] é menor que a menor distância, logo continua sendo 1 pois o número somado a ele não foi "suficiente" para chegar ao número mais próximo.

2- Avaliar o erro a expressão:

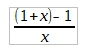
Para x ={1.e-15, 1.e+15}. Calcule os erros absolutos e relativos. Discuta a diferença nos resultados.

O programa utilizado para fazer esse exercício foi o Scilab.

Execução de iniciação:

carregando o ambiente inicial

-->x=1D-15; //Definindo o valor da variável X

-->((1+x)-1)/x //Escrevendo a expressão

ans =

1.110223

-->Erroabsoluto=abs(1-ans) //Expressão para erro absoluto

Erroabsoluto =

0.1102230

-->Errorelativo= Erroabsoluto/1 //Expressão para erro relativo

Errorelativo =

0.1102230

Execução de iniciação:

carregando o ambiente inicial

-->x=1D15; //Definindo o valor da variável X

-->((1+x)-1)/x //Escrevendo a expressão

ans =

-->Erroabsoluto= abs(1-ans) //Expressão para erro absoluto

Erroabsoluto =

-->Errorelativo=Erroabsoluto/1 //Expressão para erro relativo

Errorelativo =

No primeiro caso, quando x era muito pequeno, na ordem de 10^-15, houve um erro absoluto de 0.1102230 e um erro relativo de 0.1102230. Já quando o x é da ordem de 10^15, a expressão teve como resposta 0 tanto para o erro absoluto quanto para o erro relativo. Portanto quando o X é muito pequeno, a expressão possui um erro absoluto e relativo significativo, ou seja, o resultado da expressão é bastante impreciso quando comparado ao erro e ao resultado obtido na expressão com um valor grande de X.

3- Avalie através de um gráﬁco o valor da função

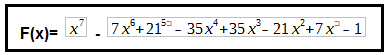
em 401 pontos equidistantes no intervalo [1−2×10−8,1+2×10−8]. Discuta.

O programa utilizado para fazer esse exercício foi o Matlab e os comandos foram

>> [((1+2e-8) -(1-2e-8)) /400] = 1.00e-10 //Operação para achar o intervalo entre os 401 pontos equidistantes

>> x=1-2e-8:1.00e-10:1+2e-8; //Definição do intervalo do gráfico x= xmin:passo:xmáx, sendo o passo, o valor encontrado na expressão anterior;

>> y=x.^7-7*x.^6+21*x.^5-35*x.^4+35*x.^3-21*x.^2+7*x-1; //F(x)

>> plot(x,y) //Comando para plotar o gráfico

>> title('Gráfico Exercício 3')

>> xlabel('x')

>> ylabel('f(x)')

>> grid on

O gráfico obtido com esses comandos foi:

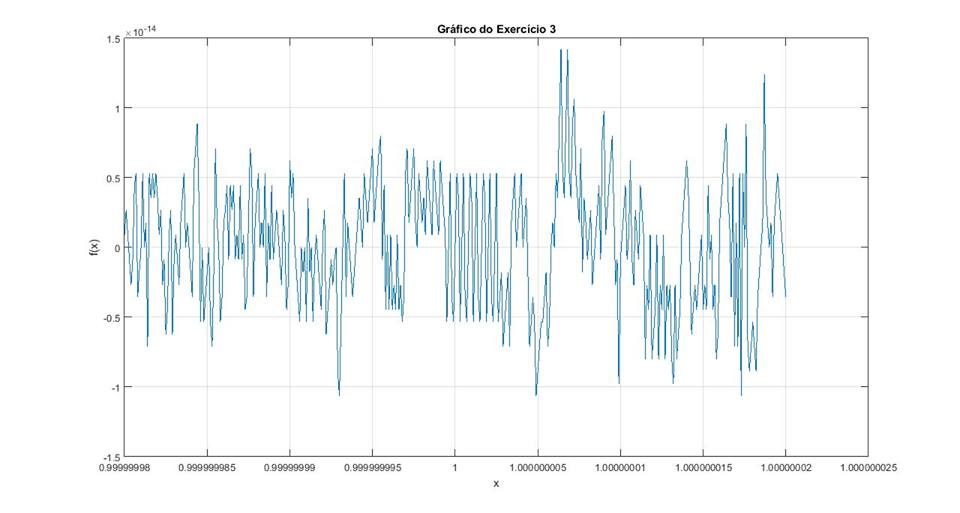
O gráfico apresentou um comportamento oscilatório que se deve ao cancelamento numérico, o qual ocorre quando existem na função, dois números com sinais opostos porém com valores absolutos muito semelhantes. Dessa forma, o resultado apresenta-se impreciso, pois devido ao arredondamento e a quantidade de algarismos utilizada pelo computador, há o cancelamento de algarismos significativos.