Lista 1B
Atividade 1B
Atividade 1B
Os exercícios dessa atividade também estão relacionados com a aritmética do ponto flutuante; erros absolutos e relativos; arredondamento e truncamento. Uma breve introdução teórica sobre esses assuntos já foi abordada e se encontra na atividade 1.
Os exercícios dessa semana foram feitos em Java.
Exercício 1
Código:
package calculo2;
import java.util.Scanner; //comando para importar classe scanner
import java.lang.Math; //comando para importar a classe matemática
public class calculo2 {
public static void main(String[] args)
{
Scanner leia= new Scanner (System.in);
int n;
System.out.println("Digite o valor de n máximo"); //comando para a pessoa digitar n
n=leia.nextInt();
double I= (1/(Math.E))*(Math.E -1); // L0, que está fora do laço
for (int i=0; i<=n; i++) //Laço com condição de início=0 e parada, quando i=n
{
I= 1-(i+1)*I;
System.out.println("Para n="+i+"I="+I); }
}}
Para alguns n, os valores obtidos com o nosso programa foi:
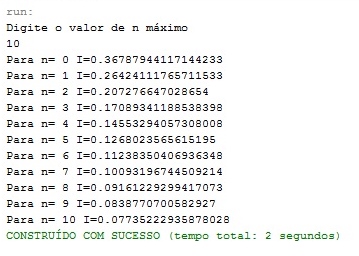
Para um valor de n=10, percebe-se que o valor de L vai convergindo para zero, como era esperado segundo o enunciado.

Para um maior valor de n, n=20, percebe-se que até n=16, L apresenta um comportamento regular, os números vão ficando cada vez menores e vão convergindo para zero; porém a partir de n=17, o módulo dos valores de L começam a aumentar, alternando- se o sinal. E como pode ser visto nas imagens a seguir, os valores de L continuam aumentando e o padrão de alteração de sinal se mantém.
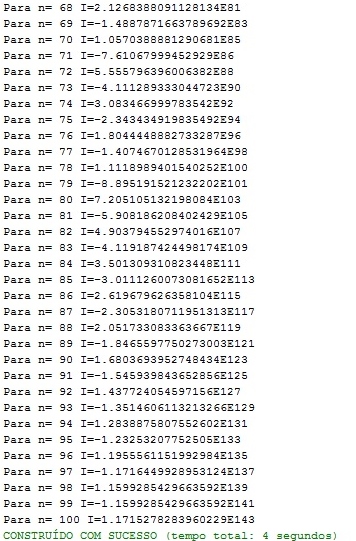

Percebe-se que após n=177, L não recebe mais valor, sendo apenas + ou - infinito. Os resultados obtidos na atividade 1 auxiliam para explicar esse comportamento. Nela, descobrimos qual era o maior número que o computador poderia representar, e esse número era 1.79x E308.
Agora analisando o resultado de L quando n=177 (o último representado) percebe-se que a ordem de grandeza desse número é muito próxima ao maior número que o computador consegue representar, dessa maneira podemos concluir que quando n=178, o computador não consegue imprimir o resultado pois ele é maior que o maior número que a máquina consegue representar. É possível concluir também que a impressão de infinito ocorre quando o valor ultrapassa o valor máximo representado pelo computador.
Em relação ao sinal, os números vão diminuindo cada vez mais até n=16, depois disso, n=17 diminui mais ainda, se tornando um valor negativo e devido operações aritméticas da própria expressão dada e regras de sinais, L apresenta essa oscilação entre um valor positivo-negativo.
Quando n tende ao infinito, l não converge para zero, como pode ser visto nas imagens acima. Porém vai ficando cada vez mais distante de zero com a alteração de sinal.
Nesse exercício, há também um erro de truncamento que se propaga desde a primeira operação realizada pelo algoritmo, quando ele calculo o I0. Isso porque o I0 tem o e (Número de Euler), e como esse é um número irracional, o computador não representa todas as casas decimais e truncando-o, propagando para todos então esse erro.
Exercício 2
Resolução
A teoria desse exercício se baseia no uso de números aleatórios e ela é conhecida como Método de Monte Carlo (MMC). É uma metodologia estatística que se embasa em uma grande quantidade de amostragens aleatórias para se chegar em resultados próximos de resultados reais, nesse caso, no valor de pi.
package exercício_2;
import static java.lang.Math.sqrt;
import java.util.Scanner;
public class Exercício_2 {
public static void main(String[] args) {
double m =0 ; //Declaração das variáveis
double n; //Declaração das variáveis
double a, b; //Declaração das variáveis
Scanner leia=new Scanner(System.in);
System.out.println("Digite o valor de n:");
n=leia.nextDouble();
for(int i=1;i<=n;i++){
double x = Math.random(); //esse comando é para gerar uma sucessão de números aleatórios entre 0,1;
double y = Math.random();
a = x*x;
b = y*y;
System.out.println("("+x+","+y+")" );
if ( sqrt(a+b) <= 1 ) // essa condição implica que se os pontos aleatórios escolhidos pelo computador estão dentro e na fronteira da circunferência de raio 1, então acumula-se um no valor de M.
{
m=m+1;
}
}
double pi = ((4*m)/n);
double ea= abs(3.1415926535897932-pi);
System.out.println("n= "+n);
System.out.println("m= "+m);
System.out.println("pi= "+ pi );
System.out.println("O erro absoluto quando n = " +n+ " é "+ea );
}
}
Nesse código, além de gerar uma sucessão de pares aleatórios e dessa maneira, valores diferentes de pi, também é possível calcular o erro absoluto. O cálculo desse último corresponde ao módulo da subtração do valor de pi usado pelo java do valor obtido no algoritmo.
Simulamos o nosso algoritmo para alguns valores de n e obtivemos os seguintes resultados:

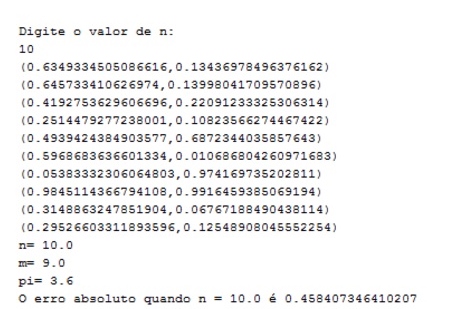
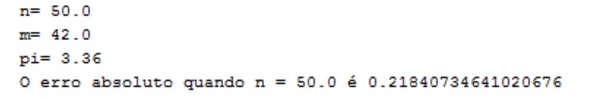

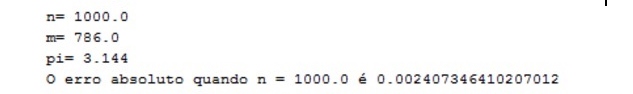
Com eles foi possível perceber que o erro absoluto diminui com o aumento de valor de n, isso ocorre porque quando o número de pares escolhidos pelo usuário é grande, ele é capaz de gerar mais pares m dentro da região delimitada, aumentando a precisão da divisão e, dessa maneira, diminuindo a diferença entre o pi obtido pela expressão e o pi representado pelo java (que é 3.1415926535897932).
Como foi dito, esse exercício baseia-se no uso de números aleatórios, então também fizemos mais simulações com o mesmo valor de n para mostrar que o valor do erro pode ser diferente para o mesmo valor de n.
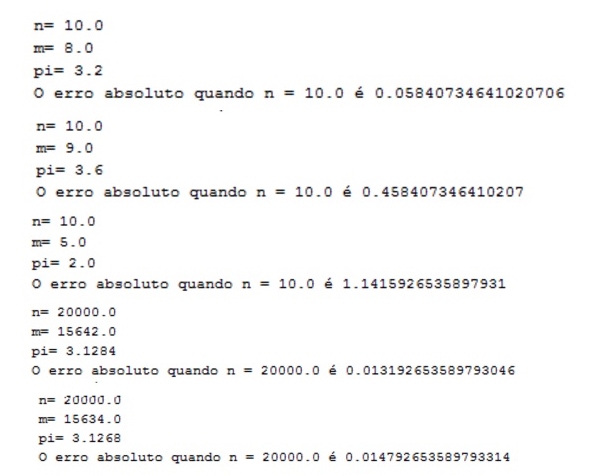
Usamos os valores de n e do erro absoluto que o algoritmo nos dava de resposta e plotamos gráficos da evolução desse erro. Como dito acima, é possível ter diferentes valores de erro para o mesmo n, então plotamos o gráficos que usavam o mesmo valor de n porém com o erro diferente para analisar o quanto a aleatoriedade poderia interferir no erro.
Para fazer os gráficos, utilizamos uma ferramenta para fazer gráfico disponível no site: <https://www.shodor.org/interactivate/activities/SimplePlot/>

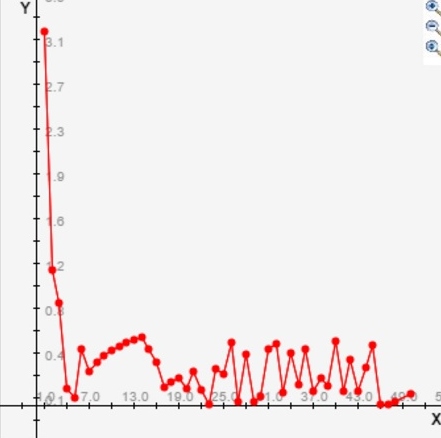
Os gráficos a cima são os gráficos de evolução de erro em função de N, e o intervalo utilizado foi [1,50] . Era esperado dois gráficos distintos, bem como obtivemos porque como a geração dos pares de m eram aleatórios, os valores de pi para cada vez que você usasse o algoritmo com o mesmo valor de n poderiam ser diferentes, obtendo então erros distintos. Apesar de ser esperado gráficos diferentes em certos pontos, o comportamento visto nos dois foi padrão. Para Ns pequenos, o erro era grande porém quando N cresce, o erro diminui. Claro que por se tratar de valores aleatórios, não necessariamente o erro associado a n=25 é menor que o erro associado a n=15. Mas a evolução do erro nesse caso é justamente ficar mais preciso, ou seja, sem valores grandes de erros associados.
Exercicío 3
O código:
import java.util.Scanner;
public class Exercício3{
public static void main (String[] args) throws
Java.lang.Exception{
int m;
Scanner leia = new Scanner(System.in);
System.out.println("Digite o valor de m: ");
m=leia.nextInt();
double pi=0;
for (int i = 0; i <= m; i++)
{
pi += ( 1.0 / Math.pow(16,i) )*( (4.0 / (8.0 * i + 1.0)) - (2.0 / (8.0 * i + 4.0)) - (1.0 / (8.0 * i + 5.0)) - (1.0 / (8.0 * i + 6.0)) );
} System.out.println("Valor de Pi: "+pi);
} }
Um valor de pi encontrado na literatura com o maior número de casas decimais é 3.1415926535897932 38462643383279502884
Alguns valores obtidos foram
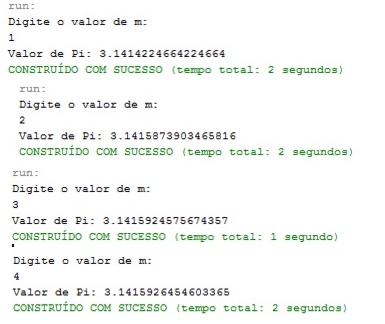

Como visto nas imagens a cima, quando m>=10, obtém-se uma aproximação que coincide com a mesmo valor de π que o java usa.
Referências
QUARTERONI, A.; SALERI, F. Cálculo Cientifico com MATLAB e Octave
