Lista 2A
Os assunto abordados na atividade 2A de cálculo numérico são zeros e funções reais. Vamos então descobrir as raízes das funções dadas nos exercícios atráves de métodos distintos porém igualmente eficazes.
Atividade 2A
MÉTODO DA BISSECÇÃO
O primeiro método que vamos falar e utilizar nos dois exercícios é o método da bissecção. Para utilizar esse método, a função analisada deve ser continua e deve ter dois pontos de partida, tal que a função tenha sinais opostos em cada um desses pontos.
Então suponha que haja uma função contínua e que se escolha dois valores aleatórios para x: x1 e x2. Se f(x1) vezes f(x2) (f(x1)*f(x2)) for menor que zero, significa que um dos valores é negativo, que implica que em algum valor de x, a função passa pelo zero, logo há uma raíz para ser calculada.
A lógica desse método então baseia-se na divisão dos intervalos pela metade até que a raiz seja encontrada.
No exemplo dado, o intervalo em que tem-se a raíz é [x1,x2]. Dividindo esse intervalo ao meio, tem-se então dois subintervalos [x1,xm(x médio)], [xm,x2].
Agora que o primeiro intervalo já foi dividido, é necessário analisar se o o ponto em que a função corta o zero está no primeiro ou no segundo subintervalo.
Há somente 3 opções:
Se F(xm)=0, então Xmédio é a raíz da função em questão;
Se f(x1)*f(xm)<0, então o ponto que se deseja encontrar está no subintervalo [x1,xm];
Se f(xm)*f(x2)<0, então a raíz está no subintervalo [xm,x2];
Se a raíz estiver no primeiro subintervalo, então xm passa a ser o limite superior, ou seja, x2=xm;
Se a raíz estiver no segundo subintervalo, então xm passa a ser o limite inferior, ou seja, x1=xm;
Depois de definido o novo limite superior ou inferior, inicia-se o processo de divisão do intervalo pela metade novamente, até que a raíz seja encontrada, como exemplificado na imagem.
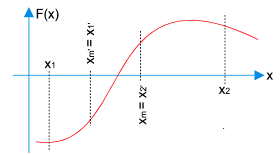
Figura 1: Divisão de subintervalos de uma função. Método da bissecção.Disponível em <https://www.mspc.eng.br/matr/im01/rmat2A09.gif>
O critério de parada para esse método pode ser quando se limita o número de iterações, divisões de intervalo, máximas e também quando o valor da raiz encontrada está dentro de um erro pré-estabelecido.
MÉTODO DE NEWTON RAPHSON
O segundo método é o de Newton-Raphson, que é um caso particular do método de iteração linear. A idéia desse método é que quando se tem uma função f(x) contínua, pode-se ter f'(a)=0 (a Derivada da função no ponto a é igual a zero) em quem a é a raiz da função em questão e que pertence a um intervalo pré-definido.
O método de Newton-Raphson garante a convergência da função mas apenas para um intervalo definido, por exemplo [x1,x2] em que contém a raíz e se a função e sua derivada forem contínuas nesse intervalo.
A cada iteração feita pelo método, há uma aproximação da raiz pela derivada.
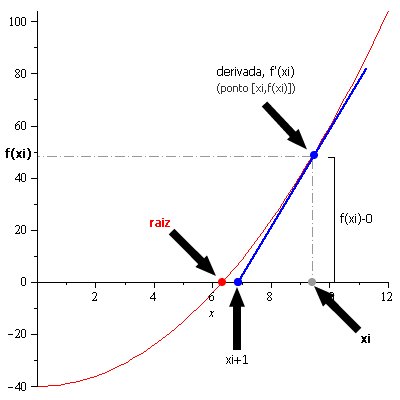
Figura 2: Aproximação da raíz pelo método de Newton Raphson. Disponível em <https://www.sawp.com.br/blog/wp-content/uploads/2010/03/fig16.png>
Nele, estimamos um valor inicial para a raiz, calculamos a derivada da função nesse ponto e realizamos a seguinte iteração:
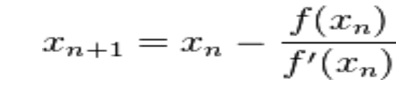
O fim da iteração é definido quando a diferença entre o valor atual da raiz e o valor anterior for menor que a tolerância do problema.
MÉTODO DA FALSA POSIÇÃO
Já o terceiro método utilizado nos execícios foi o método da Falsa Posição. Esse método é semelhante ao método das bissecções, onde se escolhe um intervalo, garantindo que a função aplicada nesse limite superior e inferior, tenham sinais opostos, a única diferença é que xn+1 é calculado pela fórmula abaixo
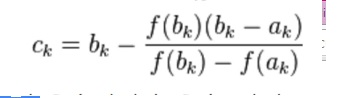
Ck é a raíz da secante. Analisando os sinais das funções do limite superior e inferior quando multiplicadas pelo valor da função calculada em Ck, encontra-se o subintervalo onde tem-se a raiz, bem como na bissecção; substitui-se o limite superior ou inferior por Ck. Esse processo é repetido até que se encontre a raíz da função.
O método da falsa posição tem convergência linear, ou seja, tende a convergir mais devagar para a solução da equação.
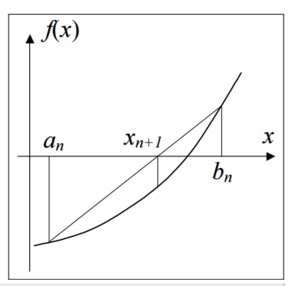
Figura 3: Gráfico que simplifica o método da Falsa posição.Disponível em <https://paginas.fe.up.pt/~faf/mnum/mnum-faf-handout.pdf>
RESOLUÇÃO DOS EXERCÍCIOS

Antes de aplicarmos os métodos para encontrarmos o volume ocupado por 1000 moléculas de gás, transformamos a equação dada em uma função
F(v)=[p+a(N/v)²(v-Nb)-KNT]
Feito isso, utilizamos a ferramenta para plotar gráfico do wolfram alpha, disponível em <https://www.wolframalpha.com/> e obtivemos os seguintes resultados
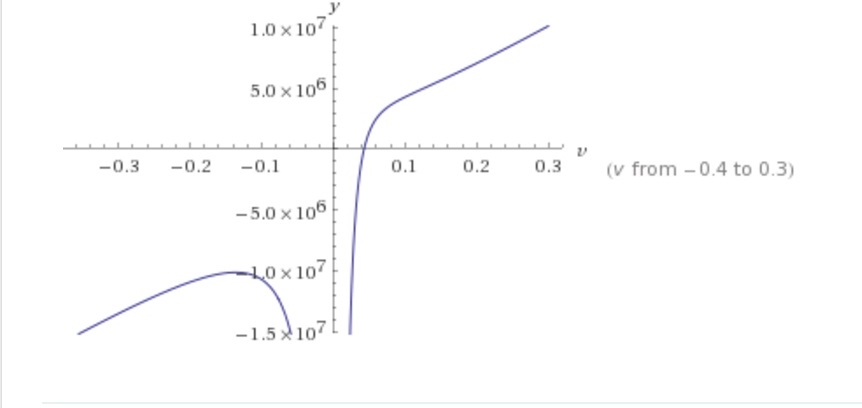
Figura 4: Gráfico da função no intervalo [-0.4, 03]
Através do gráfico pode-se ver que há duas curvas. Uma delas intercepta o eixo x, que é exatamente o ponto onde há a raíz da função e outra não intercepta o eixo x em nenhum ponto.
Para aplicarmos os 3 métodos descritos acima, temos que identificar aproximadamente onde está a raíz; ela está entre [0.01 e 0.1]. Esses são valores escolhidos arbitrariamente, poderíamos escolher quaisquer outros, contanto que a raiz esteja localizada entre esses dois pontos selecionados.
O primeiro método que usamos para encontrar a raiz foi o da Bissecção. Usamos o Scilab para fazer o algoritmo.
O algoritmo foi:
function y=fun(v) // Cria uma função
y=(3.5*(10^(7))*v)+(0.401*(1000^2)/v)-((0.401*42.7*(10^(-6))*1000^3)/(v^2))-(3.5*10^(7)*1000*42.7*10^(-6))-(1.3806503*10^(-23)*1000*300) //função desejada
endfunction
i=1
clc() //Comando para limpar o prompt de comando
a=0.01; //Limite inferior
b=0.1; //Limite superior
tolerancia=10^-12; //Tolerância dada no exercício
fa=feval(a,fun); //Definindo a função no ponto a. Esse feval está relacionado com uma múltipla avaliação de uma função para um ou dois argumentos do tipo vetor;
fb=feval(b,fun); //Definindo a função no ponto b
vr=(a+b)/2; //vr é o ponto médio entre o limite superior e inferior
Erro=100 //Erro arbitrário, para ser utilizado na condição de parada quando comparado com a tolerância, como pode ser visto no comando a baixo
while(Erro>=tolerancia)
fvr=feval(vr,fun); //calcula a função no ponto médio
caso1=fa*fvr;
caso2=fb*fvr;
if(caso1<0) //Nessa condição, caso for verdade, então Vr passa a ser o limite superior
b=vr; //limite superior passa a ser vr
fb=fvr;
valoranterior=vr; //Valor anterior passa a ser a divisão anterior feita
vr=(a+b)/2;
valoratual=vr; //Valor atual então recebe o novo valor da divisão;
end
if(caso2<0)
a=vr;
fa=fvr;
valoranterior=vr;
vr=(a+b)/2;
valoratual=vr;
end
i=i+1 //contador que será o número de iterações
Erro=abs((valoratual-valoranterior)/valoratual)*100; //erro relativo em porcentagem
printf("%1.0f%1.12f%1.12f\n",i,vr ,Erro);
end
printf("\n Raiz da equação, ou seja, o volume é =%12.10f\n",valoratual); //printar a raíz, erro e iterações
printf("Com um erro de %1.17f porcento \n",Erro);
printf("Com %d Iterações (divisões de intervalo)",i);
Os prints abaixo mostram os resultados obtidos com esse algoritmo
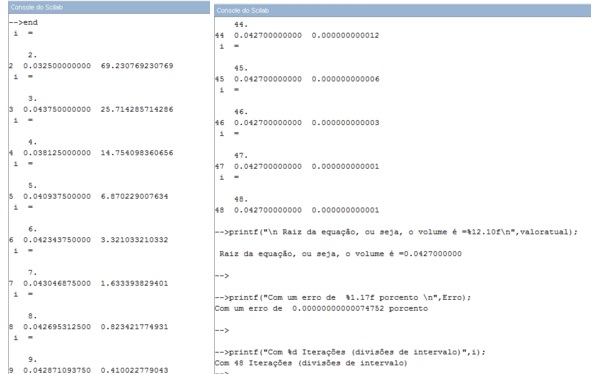
Figura 5: Simulação do algoritmo para intervlavo [0.01, 0.1]
Vemos que o algoritmo imprime no prompt de comando o número de iterações, o valor que v recebe a cada iteração o erro em porcentagem entre o valor atual de v e o valor anterior;
Com todos esses passos executados, a raiz encontrada foi de 0,0427. Ou seja, esse é o volume ocupado por 1000 moléculas desse gás.
Também podemos perceber que alterando os intervalos iniciais, o número de iterações também muda, o que pode ser visto nas imagens a baixo.
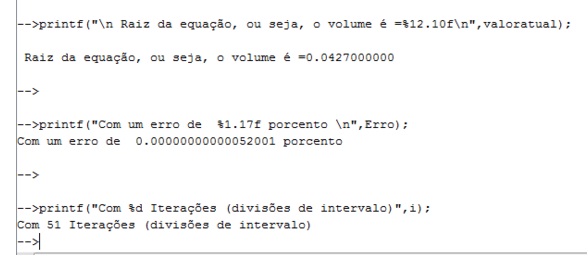
Figura 6: Simulação do algoritmo no intervalo[0.001, 0.5]
O erro em porcentagem é muito pequeno.
O segundo método para descobrir a raíz da função foi o de Newton Raphson e o algortimo foi desenvolvido na linguagem java.
O código está a baixo.
package métodonewton;
import java.util.Scanner; //importação da classe scanner.
public class Métodonewton {
public static void main(String[] args) {
int i; //declaraçao das variáveis envolvidas no problema
double chute,v;
double tolerancia=Math.pow(10,-12);
double z;
Scanner sc=new Scanner(System.in); //ler o teclado
System.out.println("Digite sua aproximação inicial para a raiz: ");
chute=sc.nextDouble(); //pede a aproximação inicial para o usuário
v=chute;
double controle=1 //a variável controle será usada para comparar a função com controle
i=1;
while (controle>tolerancia){ //laço que será executado até que o erro seja menor que a tolerância
z=v; //assumirá o valor anterior da função
v= v-(((3.5*Math.pow(10,7)+0.401*Math.pow(1000/v,2))*(v-1000*42.7*Math.pow(10,-6))-1.3806503*300)/ //f(x)
((34245.4/Math.pow(v,3))-(401000/Math.pow(v,2))+35000000)); //f'(x)
i++;
double d=z-v; //calcula a diferença a atual aproximação da função com a anterior
controle=Math.abs(d); //o módulo da diferença
}
System.out.println("A raiz, dentro da margem de tolerância, é: "+v); //mostra o valor da raiz
}
}
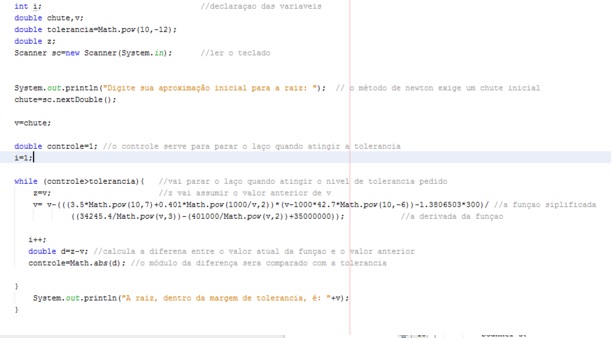
Figura 7: Print do cógido no Netbeans.
Executamos de duas maneiras distintas, em uma delas (Figura 8) mostramos todas as iterações que ocorrem até que a raíz seja encontrada.
Como pode ser visto na Figura 8, com um número muito baixo de iterações, esse algoritmo já encontra a raiz desejada dentro da tolerância.
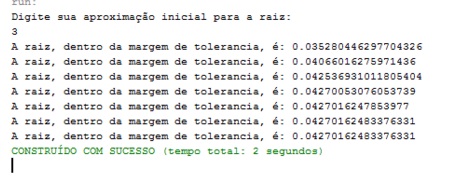
Figura 8: Iterações até encontrar a raíz desejada
Na Figura 9, temos apenas o resultado da raíz.
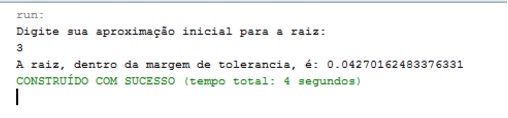
Figura 9: A raíz da função
Para saber se diferentes o chute inicial pode interferir no número de iterações feitas até que a raiz seja encontrada, rodamos o algoritmo para diferentes valores de chutes iniciais.
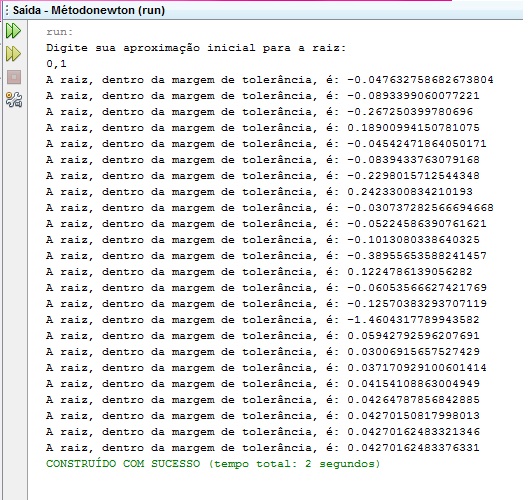
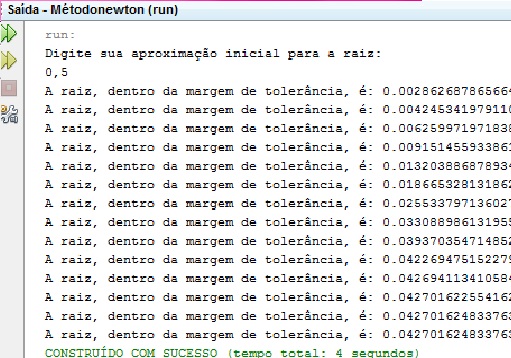
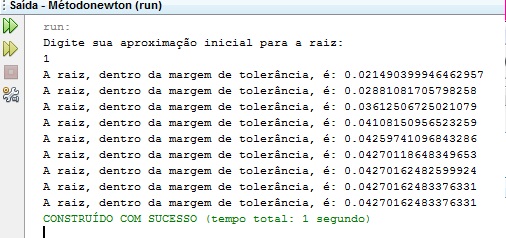
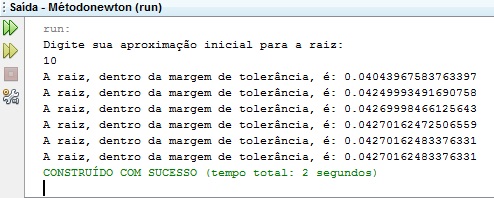
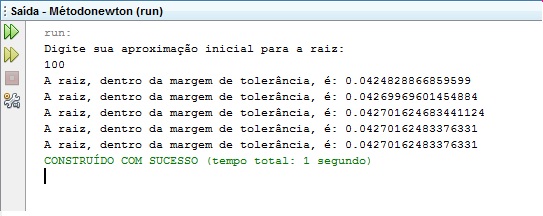
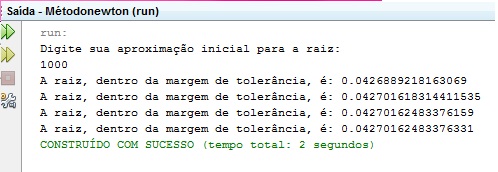
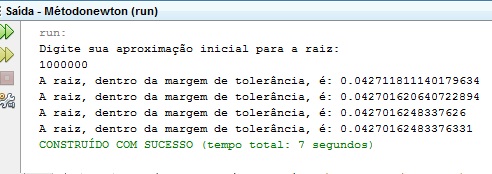
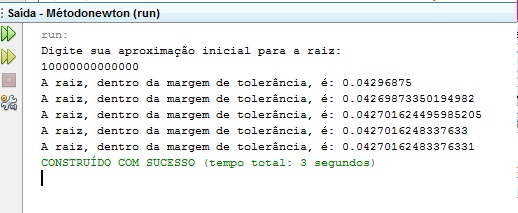
Figura 10: Simulações para diferentes valores de chute inicial.
Percebe-se que para valores pequenos do chute inicial, o método faz mais iterações para encontrar a raiz do que para valores grandes do chute inicial, ou seja, para valores grandes de chutes iniciais, função converge muito mais rapidamente do que quando usa-se valores pequenos.
O terceiro método utilizado foi o da Falsa-Posição.
Esse execício também foi desenvolvido usando-se a linguagem java.
O código:
package javaapplication40;
public abstract class funcaao {
public abstract double eval( double v);
} // Primeiro criamos uma classe java e definimos uma classe abstrata, que é apenas um modelo para a classe concreta, depois será chamada para implementar um método.
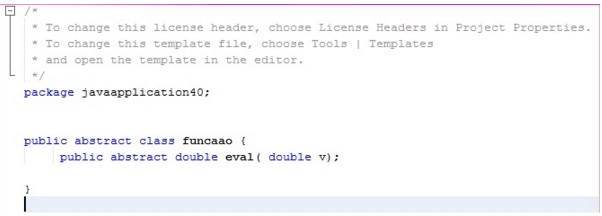
Figura 11: Criação da classe abstrata e declarando a variável v
Feito isso, criamos uma outra classe dentro desse package javaapplication40, e demos o nome de FalsaPosição.
package javaapplication40;
import java.util.ArrayList; //Importação para fazer um vetor;
public class FalsaPosição {
ArrayList iter=new ArrayList(); //Declarando o vetor que serão as iterações
public double raiz(funcaao f, double v0, double v1, int n ,double tolerancia){
double r =Double.NaN; //Valor qualquer para a raíz
double v=v0; //Valor inicial de V é o limite inferior
int k=0;
String i= "vo\tv1\tv\tf(v)";
iter.add(i);
while(Math.abs(f.eval(v))>tolerancia && k<n){
v=(v0*f.eval(v1)-v1*f.eval(v0))/(f.eval(v1)-f.eval(v0));
i= "\n"+k+"\n" + v0 + "\t" + v1 + "\t" + v + "\t" + f.eval(v);
iter.add(i);
if (f.eval(v0)*f.eval(v1)<0)
v1=v;
else
v0=v;
k++;
}
if(k<n)r=v; // No final do laço, deve retornar r;
return r;
}
public ArrayList getIter(){
return iter;
}
}
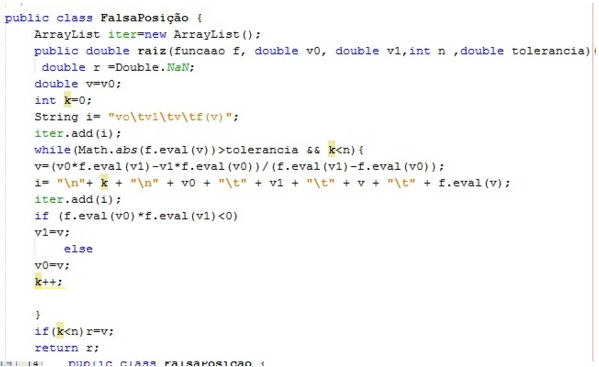
Figura 12: Parte do algoritmo da falsa posição
Depois criamos outra classe, no mesmo lugar para finalmente escrevermos a nossa função e obter o valo desejado da raíz.
public class exer1 {
public static void main(String[] args){
funcaao f=new funcaao(){
@Override //Chamada da classe abstrata
public double eval(double v) {
return
(3.5*Math.pow(10,7)*v)+((0.401*Math.pow(1000,2)/v))-(0.401*42.7*Math.pow(10,-6)*Math.pow(1000,3)/(Math.pow (v,2)))-(3.5*Math.pow(10,7)*1000*42.7*Math.pow(10,-6))-(1.3806503*Math.pow(10,-23)*1000*300); }
};
FalsaPosição rf=new FalsaPosição(); //chamada da classe Falsa Posição
double raiz=rf.raiz(f,0.01, 0.1, 700, 1e-12);
System.out.println(" Iterações são \n"+rf.getIter());
}
}
O critério de parada desse algoritmo é o número de iterações pré- estabelecido, que no caso são 700 iterações;
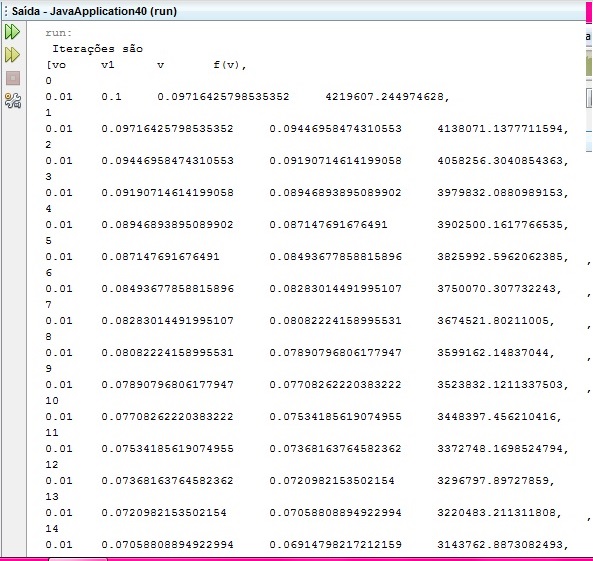
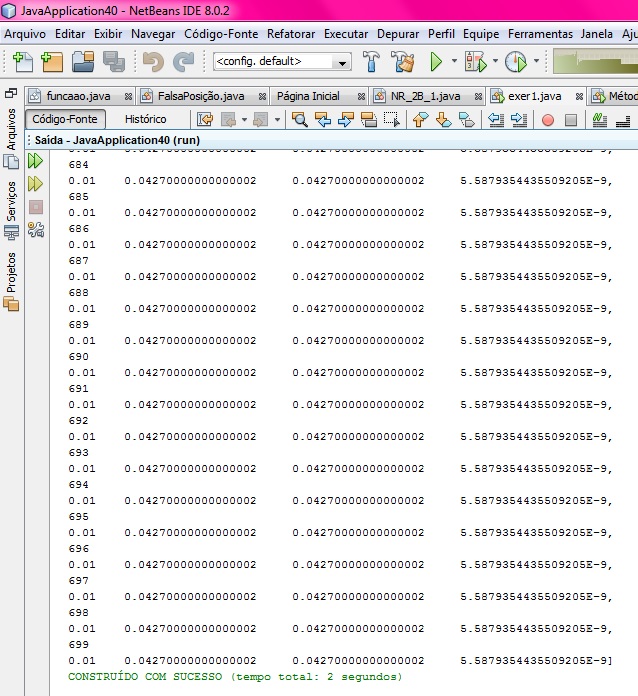
Figura 13: Iterações do algoritmo
O valor de v vai convergindo para o mesmo valor, ou seja, para o valor da raíz. 700 iterações são muitas iterações, v chega no mesmo valor na iteração de número 536.
Como são muitas iterações, disponibilizamos o arquivo Falsa posição com todos os valores que aparecem com 700 iterações.
Todos 3 métodos foram capazes de encontrar a raiz da função, que nesse caso é de 0,0427.
O que difere cada método, além de como são desenvolvidos, é a rapidez com que eles são capazes de encontrar a raiz, entre outras palavras, o modo de como eles convergem.
O método da bissecção e da falsa posição convergem de forma linear, e por isso demoram para encontrar a raiz da função. Como pôde ser visto, pela bissecção foram necessário 53 iterações e na falsa posição 536.
Já no método de Newton Raphson, foram necessárias menos interações, evidenciando que esse método converge de maneira quadrática, chegando mais rapidamente na raiz desejada.
APLICAÇÕES PARA O DIÓXIDO DE CARBONO
Sabe-se que o gás carbônico emitido principalmente pelo uso de combustíveis fósseis, é o principal culpado pelo aquecimento global, sendo ele o gás de maior emissão pelos humanos.
Frente a isso, indústria vem se revolucionando para fazer uso desse gás e consequentemente, diminuir sua emissão.
Vem sendo então desenvolvida uma molécula denominada DBN (uma base orgânica nitrogenada), que é capaz de capturar o dióxido de carbono (CO2) e convertê-lo em produtos que possam ser utilizados pela indústria química para substituir reagentes tóxicos utilizados hoje para fabricação de compostos orgânicos usados como pesticidas e fármacos.
Na indústria alimentícia, o CO2 é um agente criogênico fundamental nos processos de resfriamento, refrigeração e congelamento já que protege o sabor e a textura dos alimentos por manter o controle de temperatura apropriada. Ele também reduz reduz a necessidade de conservantes em produtos embalados e é um ingrediente essencial em bebidas carbonatadas.
Na indústria de papel e celulose, dióxido de carbono é um gás industrial usadopara controlar os níveis de pH, aumentar o rendimento da pasta e lavar o estoque de pasta crua e branqueada;
Ele também pode ser utilizado na área da saúde, para tratamento de água e na mecânica.

Para determinar o melhor intervalo para se trabalhar com os métodos, foi utilizado o site <https://pt.numberempire.com/graphingcalculator.php> para plotarmos o gráfico. Também escolhemos um valor negativo de E=-10.
O gráfico obtido foi
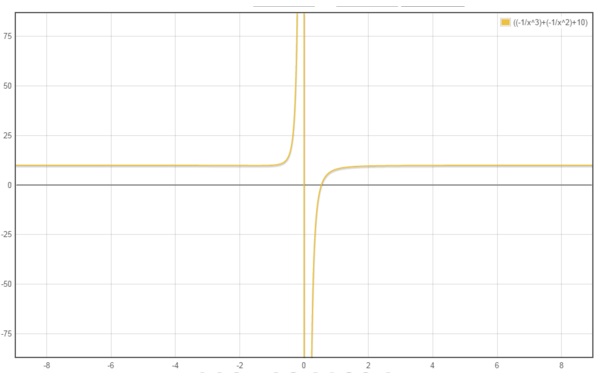
Figura 14: Gráfico da função com E=-10
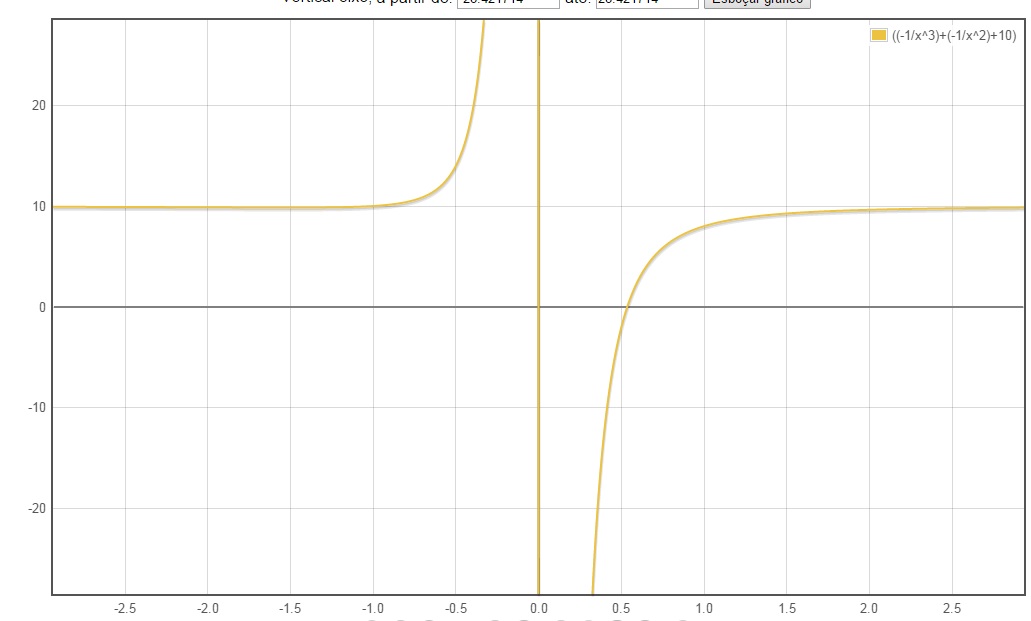
Figura 15: Gráfico da função com E=-10 com zoom.
O arquivo de Excel com os 3 métodos está disponível, para que possa ser visto e também manipulado.
O primeiro método a ser utilizado foi o da Bissecção.
Para realizarmos o método da bissecção no excel, iniciamos nomeando dez colunas como: "k", "a", "b", "x=(a+b)/2", "f(a)", "f(b)", "f(x)", "'a-b'", "EA" e "ER".
Em uma célula separada colocamos o valor de E escolhido pelo grupo, no caso -10.
Começamos a preencher a tabela pela coluna "k" que representa o número de interações. Na primeira linha colocamos 0 e na segunda 1, selecionamos essas duas células e arrastamos para baixo até alcançarmos a linha com 100. Assim cada linha dessa coluna possui um número e marca o número da interação.
Preenchemos a seguir a primeira linha da coluna "a" com o valor mínimo do intervalo no qual esperava-se encontrar a raiz da função, no caso 0,001; E a primeira linha da coluna "b" com o valor máximo do intervalo no qual esperava-se encontrar a raiz da função, no caso 1.
Segundo este método o valor de x é obtido pela média entre os pontos dentro dos quais espera-se encontrar a raiz. Assim, a primeira linha da coluna "x=(a+b)/2" será preenchida com "=(célula com o primeiro valor de a + célula com o primeiro valor de b)/2", no caso o resultado foi de 0,50005.
Em posse dos valores de "a", "b" e "x" podemos calcular os valores de "f(a)", "f(b)" e "f(x)", para isso escrevemos na primeira linha de "f(a)" a função no ponto "a", no caso "=((-1/(célula com primeiro valor de a)^3)+(-1/(célula com primeiro valor de a)^2) - ($célula com valor de E))". O $ é utilizado para fixar a célula desejada sem que ela se altere quando arrastarmos a fórmula, e deve ser colocado antes da letra e antes do número correspondente a célula escolhida, por exemplo, se a célula fosse B3 colocaríamos $B$3. Assim, obtivemos o valor de "f(a)" como -1,0001E+12. Em seguida selecionamos essa célula e arrastamos a fórmula horizontalmente para preencher a primeira linha de "f(b)" e "f(x)", conseguindo os valores de 8 e -1,9968006 respectivamente.
A coluna "'a-b'" mostra a distância entre os pontos "a" e "b", e preenchemos a primeira linha com "=ABS(célula com primeiro valor de a + célula com primeiro valor de b)", obtendo o valor de 0,9999.
Na segunda célula de "a" e de "b" colocamos condições para determinar se o valor da raiz está entre "a" e "x" ou "x" e "b". Assim, preenchemos a segunda célula de "a" com "=SE(f(a)*f(x)<0;célula com primeiro valor de a;célula com primeiro valor de x)"; e a segunda célula de "b" com "=SE(f(b)*f(x)<0;célula com primeiro valor de b;célula com primeiro valor de x)", e obtivemos o próprio valor de "a" na coluna de "a" e o valor de "x" na coluna de "b".
Puxamos as fórmulas de "x=(a+b)/2", "f(a)", "f(b)", "f(x)" e "'a-b'" para baixo até a segunda linha.
Assim, tínhamos a segunda linha de "a", "b", "x=(a+b)/2", "f(a)", "f(b)", "f(x)" e "'a-b'" preenchida; Selecionamos essa linha dessas colunas e arrastamos para baixo até a mesma linha em que "k" é 100.
Para terminarmos, preenchemos os valores de "EA" e "ER". Na primeira célula de "EA" colocamos "=ABS(célula com primeiro valor de x - célula com segundo valor de x)", obtendo o valor de 2,50E-01. Na primeira célula de "ER" colocamos "=((célula com primeiro valor de EA)/(célula com primeiro valor de x)", obtendo 3,33E-01. Selecionamos essas primeiras células preenchidas e arrastamos as fórmulas para baixo até a linha em que k é 99, pois para calcularmos o erro da linha 100 precisaríamos do valor de x da linha 101.
Após montarmos essa tabela, pudemos observar os resultados:
-O valor de x é encontrado com 53 interações, e é 0,5354866968, quando o erro chega a zero.
-Observamos ainda que a distância entre a e b é de fato sempre dividida ao meio. (Visto pela coluna "|a-b|").
-Valores de EA menores que ER.
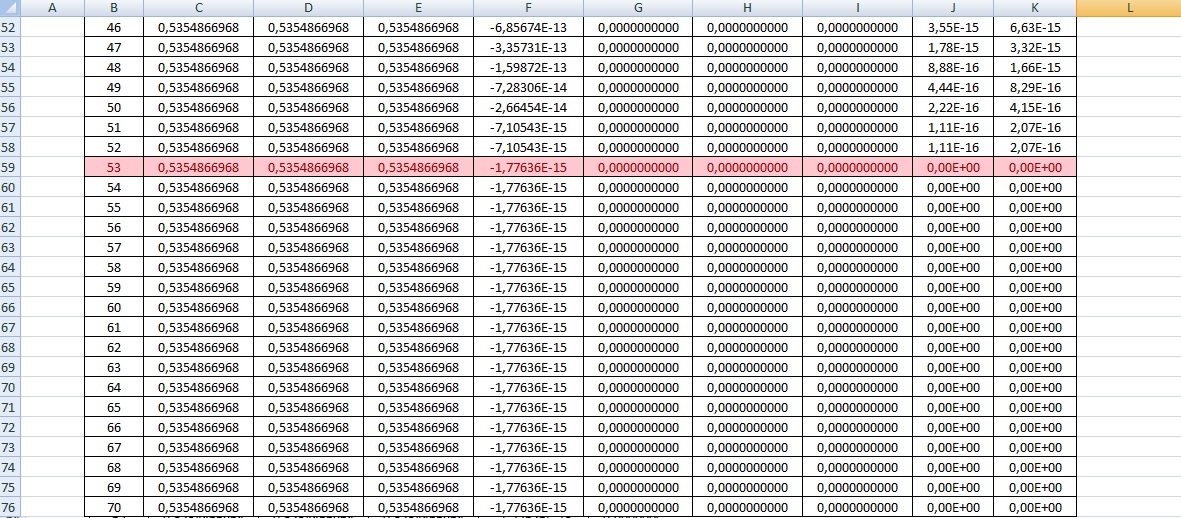
Figura 16: A raiz da função quando o erro zera
O segundo método desenvolvido no excel foi o de Newton.
Para realizarmos o método de Newton no excel, iniciamos nomeando sete colunas como: "n", "Xn", "f(Xn)", "f'(Xn)", "f(Xn)/f'(Xn)", "EA" e "ER".
Em uma célula separada colocamos o valor de E escolhido pelo grupo, no caso -10.
Começamos a preencher a tabela pela coluna "n" que representa o número de interações. Na primeira linha colocamos 0 e na segunda 1, selecionamos essas duas células e arrastamos para baixo até alcançarmos a linha com 100. Assim cada linha dessa coluna possui um número e marca o número da interação.
Preenchemos a seguir a primeira linha da coluna "Xn" com o valor perto do qual esperava-se encontrar a raiz da função, no caso 0,001.
Em posse do valor de "Xn" podemos calcular os valores de "f(Xn)", "f'(Xn)" e "f(Xn)/f'(Xn)".
Para isso escrevemos na primeira linha de "f(Xn)" a função no ponto "Xn", no caso "=((-1/(célula com primeiro valor de Xn)^3)+(-1/(célula com primeiro valor de Xn)^2) - ($célula com valor de E))". O $ é utilizado para fixar a célula desejada sem que ela se altere quando arrastarmos a fórmula, e deve ser colocado antes da letra e antes do número correspondente a célula escolhida, por exemplo, se a célula fosse B3 colocaríamos $B$3. Assim, obtivemos o valor de "f(Xn)" como -1,0001E+12.
Como f'(Xn) representa o valor da derivada da função no ponto Xn, é preciso que se derive a função primeiro, para que se possa saber em qual expressão substituir o valor de Xn, no caso a derivada de [(-1/x^3)+(-1/x^2)-(E)] é [(3/x^4)+(2/x^3)]. Preenchemos assim, a primeira célula de "f'(Xn)" com "=((3/(célula com primeiro valor de Xn)^4)+(2/(célula com primeiro valor de Xn)^3))" e obtivemos o valor de 3,0002E+16.
A primeira célula de "f(Xn)/f'(Xn)" recebeu "=célula com primeiro valor de f(Xn)/célula com primeiro valor de f'(Xn)", e o valor obtido foi -3,33344E-05.
Segundo este método o valor de x é obtido retirando de Xn o valor da divisão da função em Xn, pela derivada em Xn, do valor de Xn. Assim, a segunda linha da coluna "Xn" será preenchida com "=célula com o primeiro valor de f(Xn)/f'(Xn) - célula com o primeiro valor de Xn)", no caso o resultado foi de 0,0001333344.
Puxamos as fórmulas de "f(Xn)", "f'(Xn)" e "f(Xn)/f'(Xn)", para baixo até a segunda linha.
Assim, tínhamos a segunda linha de "Xn", "f(Xn)", "f'(Xn)" e "f(Xn)/f'(Xn)" preenchida. Selecionamos essas linha dessas colunas e arrastamos para baixo até a mesma linha em que "k" é 100.
Para terminarmos, preenchemos os valores de "EA" e "ER". Na primeira célula de "EA" colocamos "=ABS(célula com primeiro valor de x - célula com segundo valor de x)", obtendo o valor de 3,33E-05. Na primeira célula de "ER" colocamos "=((célula com primeiro valor de EA)/(célula com primeiro valor de x)", obtendo 3,33E-01. Selecionamos essas primeiras células preenchidas e arrastamos as fórmulas para baixo até a linha em que k é 99, pois para calcularmos o erro da linha 100 precisaríamos do valor de x da linha 101.
Após montarmos essa tabela, pudermos observar os resultados:
-O valor de x é encontrado com 34 interações, e é 0,5354866968.
-Valor de EA menor que ER
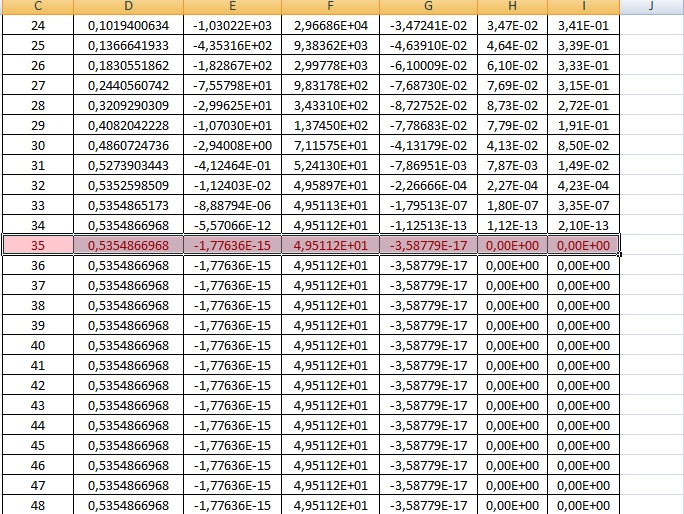
Figura 17: A partir de 35 iterações, o valor da raiz começa a ser o mesmo
Já o terceiro método foi o da Falsa posição.
Para realizarmos o método da falsa posição no excel, iniciamos nomeando nove colunas como: "k", "a", "b", "f(a)", "f(b)", "xr", "f(xr)", "EA" e "ER".
Em uma célula separada colocamos o valor de E escolhido pelo grupo, no caso -10.
Começamos a preencher a tabela pela coluna "k" que representa o número de interações. Na primeira linha colocamos 0 e na segunda 1, selecionamos essas duas células e arrastamos para baixo até alcançarmos a linha com 100. Assim cada linha dessa coluna possui um número e marca o número da interação.
Preenchemos a seguir a primeira linha da coluna "a" com o valor mínimo do intervalo no qual esperava-se encontrar a raiz da função, no caso 0,4; E a primeira linha da coluna "b" com o valor máximo do intervalo no qual esperava-se encontrar a raiz da função, no caso 0,6. Esse intervalo é diferente dos outros utilizados porque o método da falsa posição converge muito lentamente; se colocássemos os mesmos valores que colocamos para os outros, haveria uma tabela enorme, com mais de 1000 iterações; Então, julgou-se necessário escolher um intervalo mais próximo a raiz para analisar o comportamento desse método. O arquivo está disponível, caso queiram saber como esse método se comporta com outros intervalos, basta substituir os valores.
Preenchemos a primeira linha de "f(a)" com função no ponto "a", no caso "=((-1/(célula com primeiro valor de a)^3)+(-1/(célula com primeiro valor de a)^2) - ($célula com valor de E))". O $ é utilizado para fixar a célula desejada sem que ela se altere quando arrastarmos a fórmula, e deve ser colocado antes da letra e antes do número correspondente a célula escolhida, por exemplo, se a célula fosse B3 colocaríamos $B$3. Assim, obtivemos o valor de "f(a)" como -11,875. Em seguida selecionamos essa célula e arrastamos a fórmula horizontalmente para preencher a primeira linha de "f(b)", obtendo 2,5925925926.
Segundo este método o valor de x é obtido pela fórmula (1).
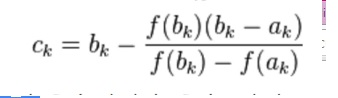
Assim, a primeira linha da coluna "xr" será preenchida com "=célula com o primeiro valor de b - [(célula com o primeiro valor de f(b)*(célula com o primeiro valor de b - célula com o primeiro valor de a))/(célula com o primeiro valor de f(b) - célula com o primeiro valor de f(a))]", no caso o resultado foi de 0,5641600000.
Em posse do valor "xr" podemos calcular os valores de "f(xr)", para isso escrevemos na primeira linha de "f(xr)" a função no ponto "xr", no caso "=((-1/(célula com primeiro valor de xr)^3)+(-1/(célula com primeiro valor de xr)^2) - ($célula com valor de E))". O $ é utilizado para fixar a célula desejada sem que ela se altere quando arrastarmos a fórmula, e deve ser colocado antes da letra e antes do número correspondente a célula escolhida, por exemplo, se a célula fosse B3 colocaríamos $B$3.
Na segunda célula de "a" e de "b" colocamos condições para determinar se o valor da raiz está entre "a" e "x" ou "x" e "b". Assim, preenchemos a segunda célula de "a" com "=SE(f(a)*f(x)<0;célula com primeiro valor de a;célula com primeiro valor de x)"; e a segunda célula de "b" com "=SE(f(b)*f(x)<0;célula com primeiro valor de b;célula com primeiro valor de x)", e obtivemos o próprio valor de "a" na coluna de "a" e o valor de "x" na coluna de "b".
Puxamos as fórmulas de "f(a)", "f(b)", "xr" e "f(xr)" para baixo até a segunda linha.
Assim, tínhamos a segunda linha de "a", "b", "f(a)", "f(b)", "xr" e "f(x)" preenchida; Selecionamos essa linha dessas colunas e arrastamos para baixo até a mesma linha em que "k" é 100.
Para terminarmos, preenchemos os valores de "EA" e "ER". Na primeira célula de "EA" colocamos "=ABS(célula com primeiro valor de x - célula com segundo valor de x)", obtendo o valor de 1,61E-02. Na primeira célula de "ER" colocamos "=((célula com primeiro valor de EA)/(célula com primeiro valor de x)", obtendo 2,85E-02. Selecionamos essas primeiras células preenchidas e arrastamos as fórmulas para baixo até a linha em que k é 99, pois para calcularmos o erro da linha 100 precisaríamos do valor de x da linha 101.
Após montarmos essa tabela, pudermos observar os resultados:
-O valor de x é encontrado com 39 interações, e é 0,5354866968.
-Valores de EA menores que ER.
-Valores iniciais tiveram que ser mais próximos do valor da raiz.
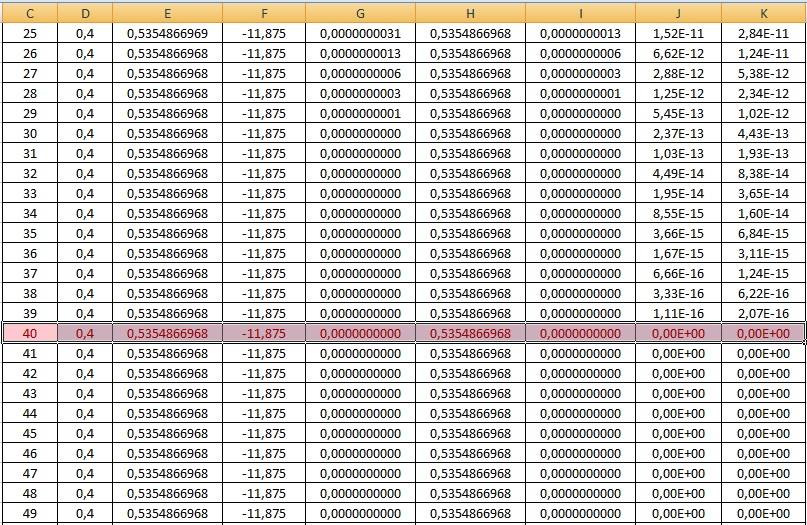
Figura 18: A partir de iterações=40, o erro relativo e absoluto passam a ser zero
Comparando os 3 métodos e os resultados obtidos é possível chegar a mesma conclusão que do exercício 1. Todos os métodos são capazes de encontrar a raiz da função em questão. O método de Newton, como pôde ser visto, mais uma vez convergiu mais rapidamente para a raiz da função, com 35 iterações; O método da bissecção convergiu com 53 iterações; O da falsa posição com o mesmo intervalo não pôde ser determinado por demorar muito até chegar na raiz desejada.
Para comparar essa rapidez com o qual cada método encontra sua raiz, plotamos gráficos para os três métodos f(x) X N (Número de iterações). Para que fosse possível realizar essa comparação, foram alterados os intervalos do método da bissecção e o valor inicial do método de newton para os mesmos valores do método da falsa posição.
Os gráficos obtidos foram
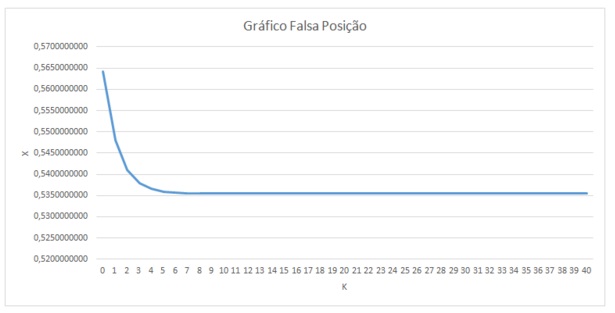
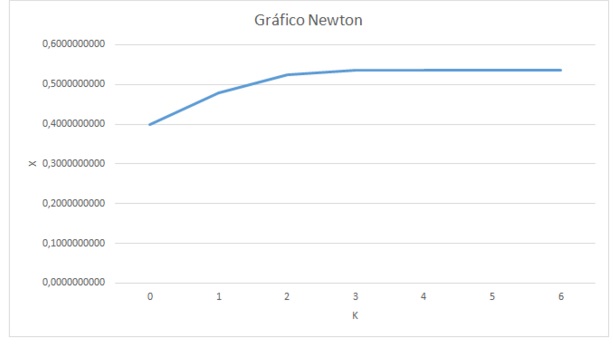
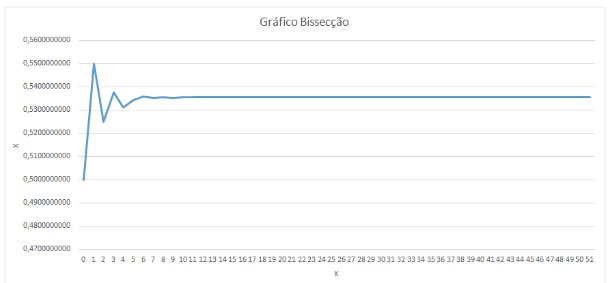
Os gráficos apenas demonstram mais uma vez que o método de newton é o mais rápido para descobrir raízes de função e esse comportamento é devido a convergência desse método ser quadrática.
