Para o primeiro exercício, foi requerido que nós usássemos o método de Newton-Raphson e outro à nossa escolha. No caso, decidimos usar o método da bisseção. Ambos já foram explicados na atividade anterior. Os dois algoritmos foram desenvolvidos utilizando a linguagem java.

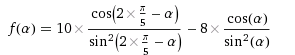
Derivada:

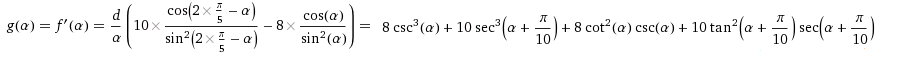
NEWTON-RAPHSON

Código:

package javaapplication3;

import java.util.Scanner;

public class JavaApplication3 {

 //Definindo a função f(a)

public static double f(double a) {

double pi = 3.141592653589793238462643383279502884197169399375105820974;

return ((10 * (Math.cos(pi - ((3 * pi) / 5) - a) / Math.pow(Math.sin(pi - ((3 * pi) / 5) - a), 2))) - (8 * ((Math.cos(a)) / Math.pow(Math.sin(a), 2))));

}

//Definindo a função g(a) = f'(a)

public static double g(double a) {

double pi = 3.141592653589793238462643383279502884197169399375105820974;

return ((8 * (Math.pow(1 / (Math.sin(a)), 3)))

+ (10 * Math.pow(1 / Math.cos(a + (pi / 10)), 3))

+ (8 * (Math.pow(1 / Math.tan(a), 2)) * (1 / Math.sin(a)))

+ (10 * (Math.pow(Math.tan(a + (pi / 10)), 2)) * (1 / Math.cos(a + (pi / 10)))));

}

//Agora deifinímos o metodo de Newton-Raphson

public static double NR_2B_1() {

int i = 1;

double x, y;

Scanner sc = new Scanner(System.in);

System.out.println("De um chute inicial para x0:");

y = sc.nextDouble();                                                 //Pedimos para o usuário definir o valor de Y;

x = 0;

while (y != x && Math.abs(y - x) > Math.pow(10, -14)) {

x = y;

y = x - (f(x) / g(x));

System.out.println("A raíz é: " + y + " na " + i + "ª iteração.");

i++;

}

return y;

}

public static void main(String[] args) {

double r;

r = NR_2B_1(); //Chamamos o método NR_2B_1

}

}

Resultados

Para x0 = 0.1 :

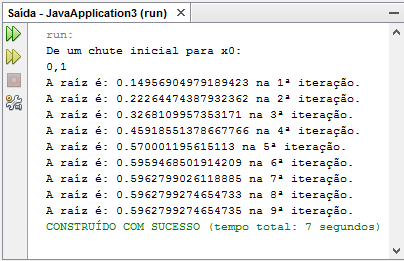
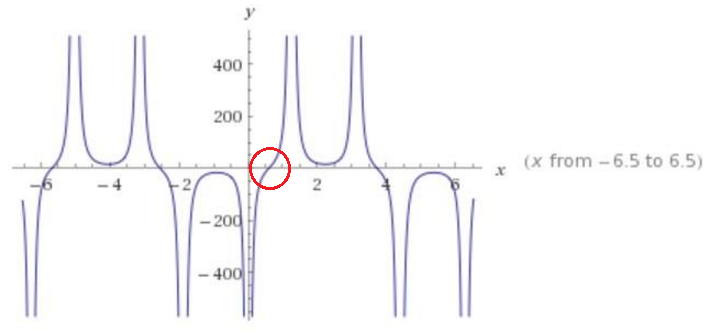
-Neste caso, podemos observar que o valor obtido para a raiz converge rapidamente para o valor do zero da função, observado no gráfico. 

Para o caso x0 = -6

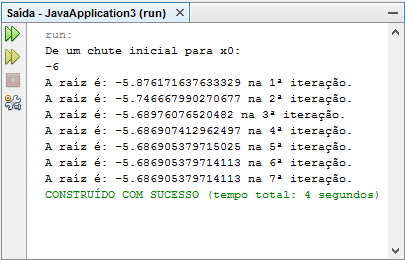
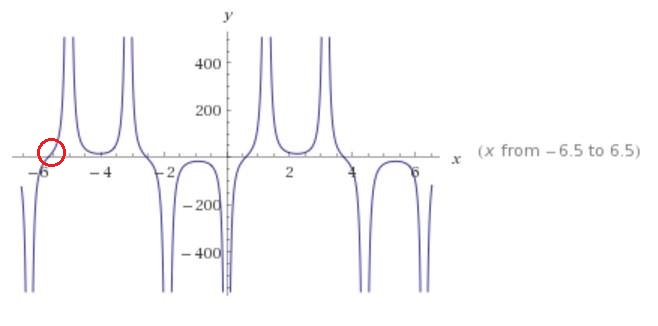
-Neste caso, podemos notar que, novamente, o valor dado pelo programa e o valor do gráfico são bastante próximos.

BISSEÇÃO

Código:

package bissecao2b;

import java.util.Scanner;

public class Bissecao2b {

public static void main(String[] args) {

double x1, x2;

double pi = 3.141592653589793238462643383279502884197169399375105820974;

Scanner sc = new Scanner(System.in);

System.out.print("Digite o primeiro valor do intervalo :");

x1 = sc.nextDouble();

System.out.print("Digite o segundo valor do intervalo :");

x2 = sc.nextDouble();

int i = 0;

double aux;

double y1 = ((10 * (Math.cos(pi - ((3 * pi) / 5) - x1) / Math.pow(Math.sin(pi - ((3 * pi) / 5) - x1), 2))) - (8 * ((Math.cos(x1)) / Math.pow(Math.sin(x1), 2))));

double y2 = ((10 * (Math.cos(pi - ((3 * pi) / 5) - x2) / Math.pow(Math.sin(pi - ((3 * pi) / 5) - x2), 2))) - (8 * ((Math.cos(x2)) / Math.pow(Math.sin(x2), 2))));

while ((y1 < 0 && y2 < 0) '' (y1 > 0 && y2 > 0)) {//

System.out.println("É impossível identificar raízes nesse caso pois ambos os valores de f(x) possuem o mesmo sinal."

+ "Por favor, apresente outros");

System.out.print("Digite o primeiro valor do intervalo :");

x1 = sc.nextDouble();

System.out.print("Digite o segundo valor do intervalo :");

x2 = sc.nextDouble();

y1 = ((10 * (Math.cos(pi - ((3 * pi) / 5) - x1) / Math.pow(Math.sin(pi - ((3 * pi) / 5) - x1), 2))) - (8 * ((Math.cos(x1)) / Math.pow(Math.sin(x1), 2))));

y2 = ((10 * (Math.cos(pi - ((3 * pi) / 5) - x2) / Math.pow(Math.sin(pi - ((3 * pi) / 5) - x2), 2))) - (8 * ((Math.cos(x2)) / Math.pow(Math.sin(x2), 2))));

}

while (Math.abs(y1 - y2) > Math.pow(10, -10)) {

if ((y1 < 0 && y2 > 0) '' (y1 > 0 && y2 < 0)) {         //SINAIS DIFERENTES

aux = x2;

x2 = (x1 + x2) / 2;

y2 = ((10 * (Math.cos(pi - ((3 * pi) / 5) - x2) / Math.pow(Math.sin(pi - ((3 * pi) / 5) - x2), 2))) - (8 * ((Math.cos(x2)) / Math.pow(Math.sin(x2), 2))));

if ((y1 < 0 && y2 < 0) '' (y1 > 0 && y2 > 0)) {               //SINAIS IGUAIS

x2 = aux;

x1 = (x1 + x2) / 2;

y1 = ((10 * (Math.cos(pi - ((3 * pi) / 5) - x1) / Math.pow(Math.sin(pi - ((3 * pi) / 5) - x1), 2))) - (8 * ((Math.cos(x1)) / Math.pow(Math.sin(x1), 2))));

y2 = ((10 * (Math.cos(pi - ((3 * pi) / 5) - x2) / Math.pow(Math.sin(pi - ((3 * pi) / 5) - x2), 2))) - (8 * ((Math.cos(x2)) / Math.pow(Math.sin(x2), 2))));

}

}

System.out.println(x2);

i++;

}

System.out.println("O valor obtido da raiz é: " + x2);

System.out.println("O número total de iterações foi: " + i);

}

}

Resultados

Para o intervalo {0,1; 2}

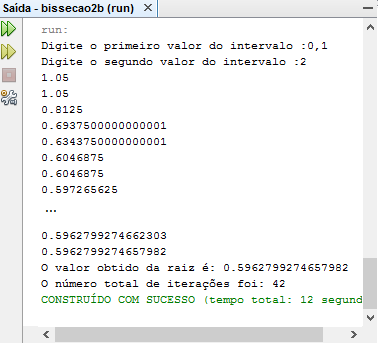
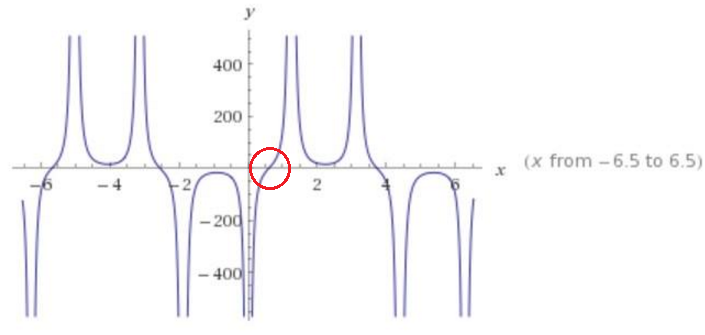
-O valor obtido por esse método foi muito próximo ao valor obtido pelo método de Newton, divergindo apenas da quantidade de iterações necessárias até se encontrar a raiz.

Para o intervalo inválido {2;2,5} e depois para o intervalo {-6;-5}.

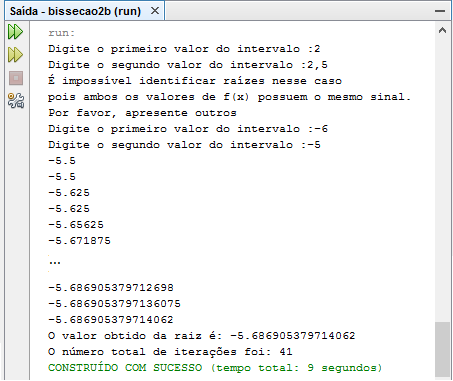
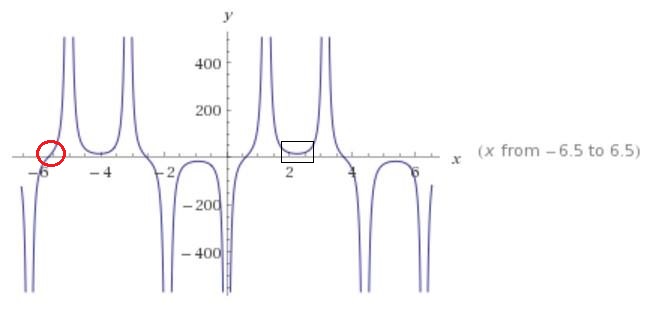
-Esse exemplo mostra como, caso o usuário apresente variáveis que formem um intervalo no qual não há raízes, o programa acusa o erro e pede para que o usuário apresente novas variáveis. Novamente a raíz encontrada condiz com o que observamos, tanto na figura, quanto no método de Newton-Raphson.

Conclusão

Iteração de ponto fixo

 Mas o que é ponto fixo? Ponto fixo de dada função F  é o número  x* que quando usado na função resulta nele mesmo, ou seja, F(x*)=x*. Dada uma aproximação inicial X0  para x*, o método consiste em iterar sucessivamente a função dada sobre X0 . Ou seja, constrói-se a sequência X(n+1)=Fn+1(X0)=Fn(F(X0)) sendo cada Xn  uma nova aproximação do ponto fixo x*. Dada uma função f(x) contínua no intervalo [a,b] onde existe uma raiz única, f(x) = 0, é possível transformar tal equação em uma equação equivalente x = g(x) e, a partir de uma aproximação inicial x0, gerar uma seqüência {xk} de aproximações para x pela relação xk+1 = g(xk), uma vez que g(x) é tal que f(x) = 0, se e somente se g(x) = x.

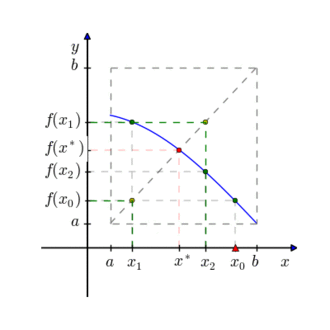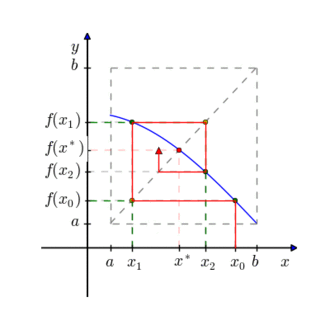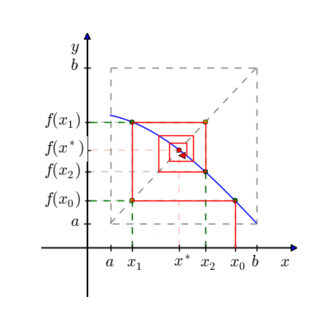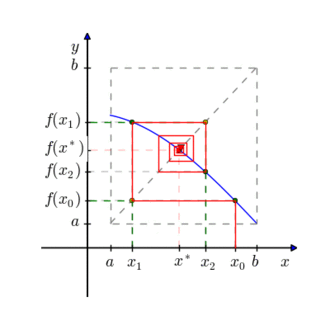
O algoritmo foi desenvolvido em linguagem java e o código encontra-se abaixo:

Código:

package exe.pkg22b;  

import static java.lang.Math.abs;

import java.util.Scanner;

public class Exe22b {

public static void main(String[] args) {

double R;

double xi;

int n;

double tolerancia=Math.pow(10,-16);                    //Tolerância arbitrária escolhida pelo grupo

Scanner sc=new Scanner(System.in);

System.out.println(" Digite o número que você gostaria de saber a raiz:\n");

R=sc.nextDouble();

System.out.println(" Digite a aproximação para o ponto fixo:\n");

xi=sc.nextDouble();

int k=1;

n=100000;

while(k<=n){

double xk=xi*((Math.pow(xi,2))+3*R)/(3*(Math.pow(xi,2))+R);

if( abs (xk-xi)<tolerancia){

System.out.println("o número de iterações é " + k);

System.out.println("A raíz do número desejado é :" + xk);

break;

}

else {

k++;

xi=xk;

}}}}

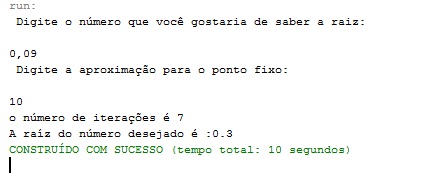
Fazendo simulações com valores aleatórios, os resultados obtidos com o algoritmo foram: 

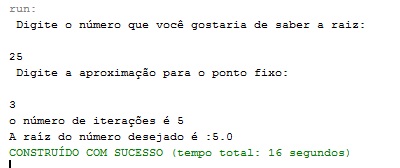
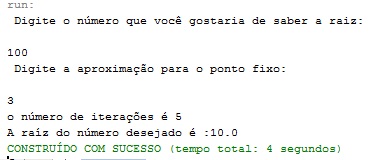
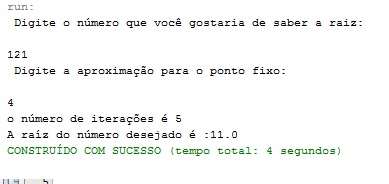
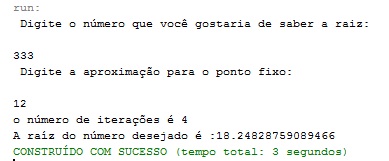
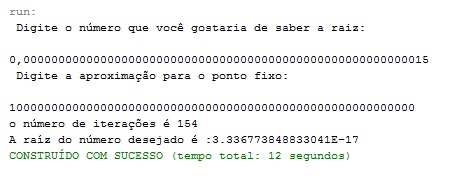
Para esses valores, houve a rápida convergência para o valor da raiz desejada. Porém, quando se escolhe um valor grande para se descobrir a raiz com uma aproximação muito pequena, o programa fica rodando, encerra e não apresenta nenhum resultado, ou seja,  mesmo com esse valor de n muito grande, não se chega em valor algum, isso deve-se porque para esses valores digitados, não se satisfaz a inequação que garante a convergência. Como pode ser visto nas imagens abaixo:

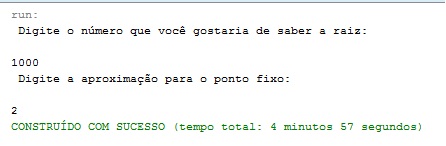
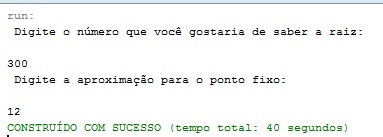
Percebam o tempo de execução, é muito grande.

Mas quando inicializamos com um valor verdadeiramente próximo a raiz, obtemos os resultados que queremos:

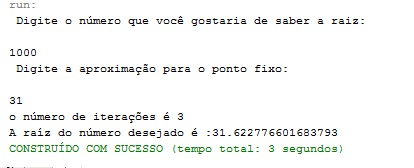
Porém quando digitamos um número maior que um que não convergiu para a raíz, com a mesma aproximação, obtivemos o seguinte resultado

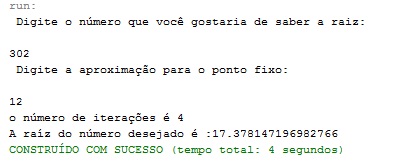
Isso não está relacionado então com o número de n, que não é suficientemente grande para que haja convergência até o valor da raíz dentro da tolerância estabelecida. Esse comportamento está relacionado com o fato de o valor inicial do número que se deseja saber a raiz e a aproximação não estão na região onde a inequação é satisfeita(inequação relacionada com o teorema da convergência, explicada a baixo), dessa maneira, eles não convergem.

O teorema da convergência afirma que se a derivada da função for x(k+1) <1 , x(k+1) e x(k+1)  forem contínuas  e x1 estiver dentro do intervalo definido, então a função vai convergir. 

Feita essa derivada e resolvida a inequação, os valores obtidos para a e para X são apresentados no gráfico abaixo, feito no wolfram

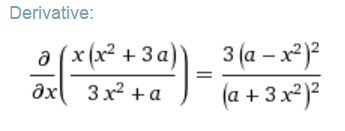
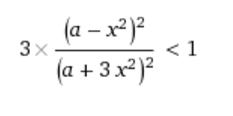
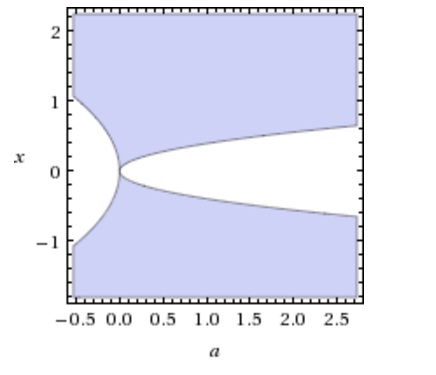
A parte em roxo representa a área em que a inequação é satisfeita.Podemos ver pelo gráfico que para a=0 e x=0, a função não converge. É também possível perceber que área de valores negativos de a, a região que não converge, aumenta mais rapidamente do que e região com a positivo.

Com as simulações abaixo podemos verificar essa convergência.

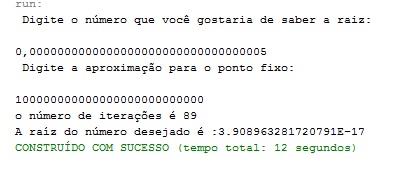
Com as imagens vistas acima, é possível concluir que mesmo com uma grande diferença entre valor do número e a aproximação linear, há sempre a convergência, se os valores escolhidos estão dentro da região onde a inequação é satisfeita. Os valores de raíz que não forem encontrados, é porque não há convergência quando combinado esses dois valores. O encontro rápido do valor desejado, com baixo número de iterações, indica que não é um método de convergência linear e sim um método de convergência de pelo menos ordem 2, como o método de Newton-Raphson.

Fazendo-se uso do teorema da convergência, pudemos chegar nos valores desejados, ou seja, o método de iteração de ponto fixo também é um método, bem como método de Newton e da bissecção apresentados nessa lista, muito eficiente para se encontrar o valor que deseja.