Lista 4
O tema abordado nessa atividade é ajustamento de curvas. Como o próprio nome diz, é um método que tenta encontrar uma curva que se ajuste a pontos e que possivelmente cumpra uma série de parâmetros adicionais.
Ajuste de curvas
Quase sempre no nosso dia-a-dia usamos tabelas para listar valores obtidos por meio de observação ou de algum processo experimental, porém a tabela em si não permite que sejam obtidos outros valores além daqueles que já estão presentes na mesma, ou seja, diferentemente de uma função, não é possível, somente com os valores da tabela obter valores que não estão explícitos. Há então um problema: Como passar a tabela para uma equação matemática que possa ser resolvida e que descreva o comportamento do fenômeno observado?
O processo no qual relaciona-se uma tabela à uma equação matemática é chamado interpolação.
Porém a interpolação não é aconselhável quando é preciso obter um valor aproximado da função em algum ponto fora do intervalo de tabelamento, ou seja, quando se quer extrapolar e também quando os valores tabelados são resultados de algum experimento físico ou de alguma pesquisa, porque, nestes casos, esse valores poderão conter erros inerentes que, em geral, não são previsíveis.
Então surge a necessidade de ajustar a essas funções tabeladas uma função que seja uma boa aproximação para os valores tabelados e que nos permita "extrapolar" com certa margem de segurança.
Para fazer essa boa aproximação, é possível usar o método dos mínimos quadrados.
Método dos mínimos quadrados
Após obter os dados da tabela que se deseja estudar, cria-se um gráfico dos pontos em um sistema de coordenadas retangulares. O conjunto resultante chama-se diagrama de dispersão e muitas vezes por ele, é possível visualizar uma curva aproximativa dos dados.
É possível ajustar mais de uma curva aos valores na tabela mas para que cada um não escolha qualquer curva, usa-se a melhor reta, melhor curva.
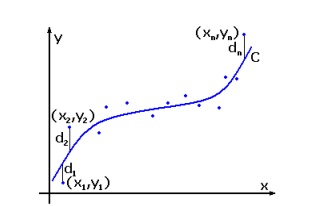
Tome os pontos e o gráfico a cima como exemplo.
Mas como saber qual o ponto em que a curva C passa? Para qualquer valor de X, por exemplo x1, haverá uma diferença entre o y1 e o y determinado pela curva C. Essa diferença é chamada de D1 e é o erro ou desvio.
Então para os valores de X, tem-se um Y associado. Com a diferença entre a reta C, é possível obter:
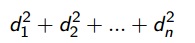
Quando a soma das distâncias ao quadrado for mínima, encontrou-se a melhor curva ajustadora e é chamada curva de mínimos quadrados, podendo ser uma reta, uma parábola, etc.
Então para se usar o método dos mínimos quadrados, primeiro é preciso colocar os pontos no gráfico e identificar se eles se assemelham de uma reta, parábola, etc. Feito isso, escolhe-se a função de ajuste. Se for uma reta temos a equação de reta:
y=a+bx
Em que a e b são os coeficientes que temos que determinar
Os valores de Y na reta de mínimos quadrados são:
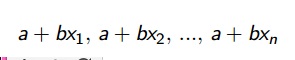
Então as diferenças são
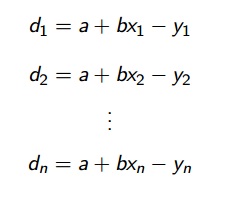
Onde y1, y2,...,yn correspondem a distância entre a reta e o ponto da tabela.
Agora temos que somar essas distâncias ao quadrado, ou seja:
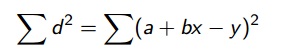
Esse somatório, é uma função de a e de b então também pode ser descrito como :
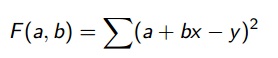
Para que esse somatório seja mínimo, e portanto a reta ser uma reta de mínimos quadrados é preciso que :
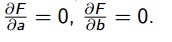
Então obtêm-se que:
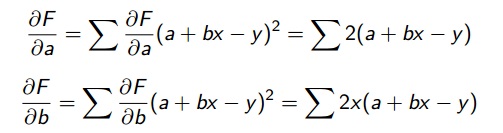
Então:
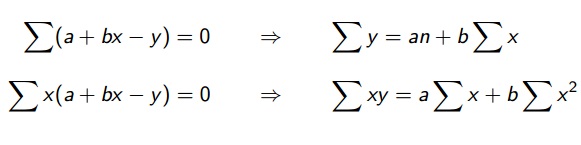
Para determinar a e b é preciso desenvolver as equações normais para a reta de mínimos quadrados:
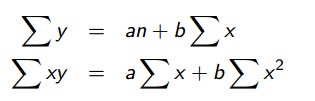
Os valores de a e b obtidos são
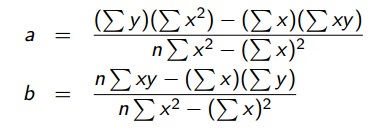
Em alguns casos, as funções escolhidas pode ser não lineares nos parâmetros, como por exemplo, se o diagrama de dispersão se ajustar a uma exponencial. Então é preciso efetuar uma linearização para que se possa aplicar o método de mínimos quadrados.
Na imagem a baixo há um exemplo de linearização

Resolução dos exercícios



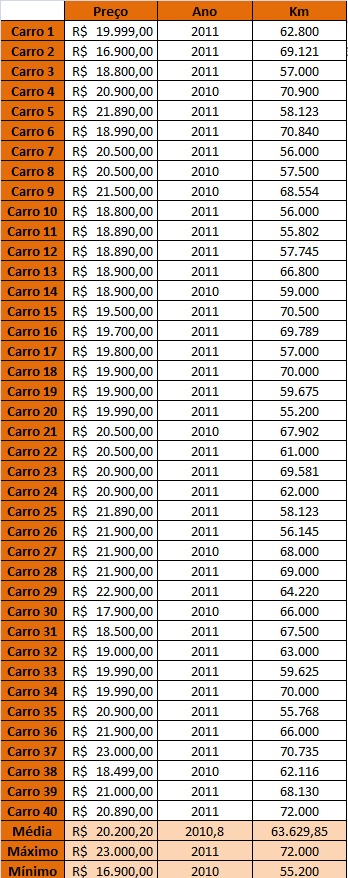

Após localizarmos os valores máximos e mínimos para preço, ano e quilometragem, calculamos Pi, Ai e Ki no excel e obtivemos os seguintes valores
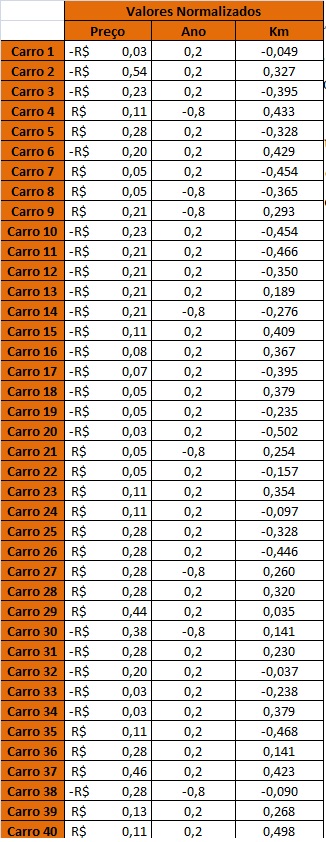

Para encontrar os respectivos coeficientes, como já estávamos com a tabela pronta no Excel, utilizamos uma função que esse programa possui para nos auxiliar. A função é a Regressão.
Essa função se baseia no método dos mínimos quadrados.
Após escolhido essa função, selecionamos os respectivos valores Y para o preço, e X para quilometragem e ano. Após isso, selecionamos nova planilha e o restultado obtido foi:
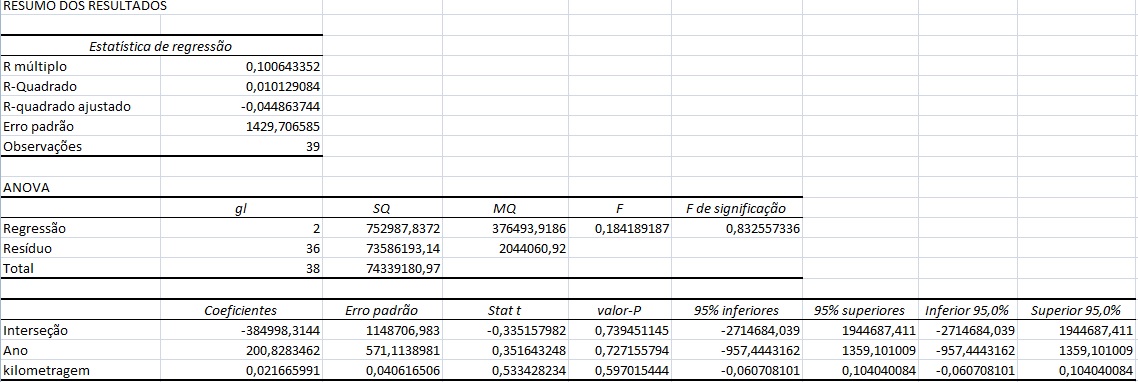
Essa nova planilha nos forneceu os valores dos coeficientes e eles são:
C0=-384998,3144
C1=200,8283462
C2=0,021665991
Portanto a função é:
P=-384998,3144+200,8283462*A+0,021665991*K

Para avaliar se a função é preciso calcular o erro quadrático médio, dado pela fórmula:
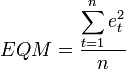
Utilizando o Excel, para cada valor de kilometragem e ano, foram calculados os preços a partir da equação de P encontrada no item anterior:
P=-384998,3144+200,8283462*A+0,021665991*K
Depois, foram calculados os erros equivalentes para cada carro, através da fórmula:
Erro absoluto = abs (preço tabelado - preço calculado)
Em seguida, esses erros foram elevados ao quadrado. Todos os valores foram colocados na tabela abaixo:
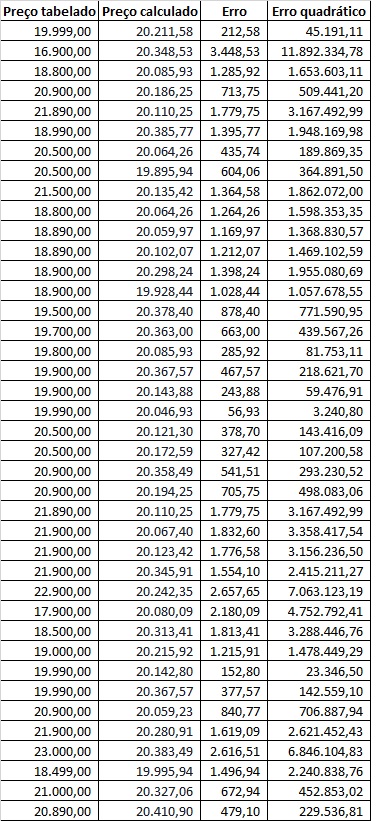
Por fim, foram somados os erros quadráticos, e depois dividido por 40. Encontrando-se, então, o erro quadrático médio (EQM).

Como o EQM possui um valor muito alto, a função utilizada por Ana não foi uma boa escolha, pois ela possui um erro muito elevado.

Ainda com a planilha eletrônica Excel, aproveitamos a tabela do exercício anterior para calcular o agio de cada anúncio. O agio foi calculado como descrito no enunciado e obtivemos os seguintes resultados
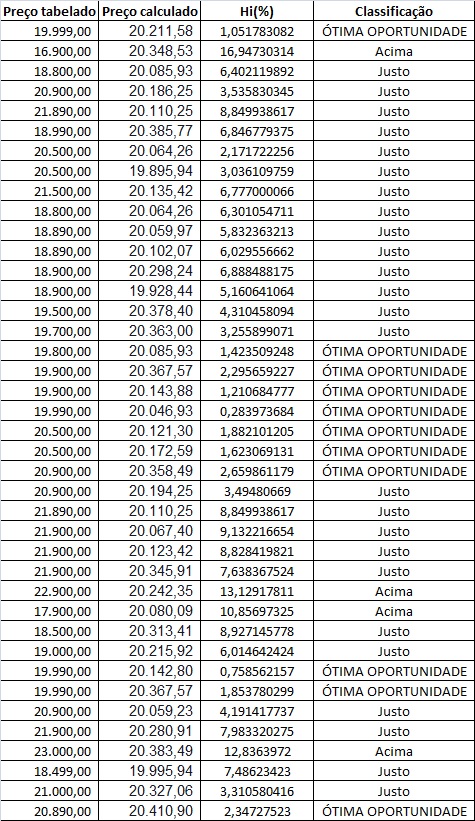
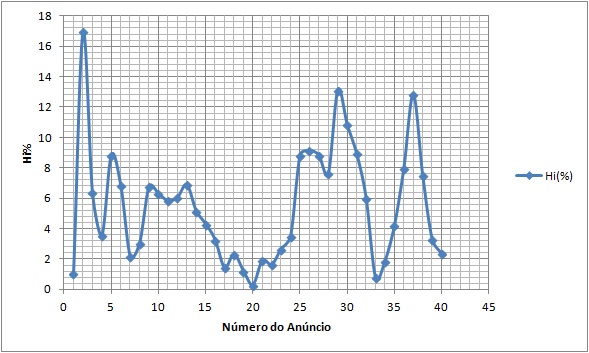
Pelo Gráfico é possível perceber que a melhor barganha é aquela que se encontra mais próxima de zero, que no caso é o anúncio número 20 com uma porcentagem de 0,28% aproximadamente.

Para descobrirmos a depreciação esperada para cada 10000km rodados, pegamos um valor aleatório d e fomos acrescentando 10000 e substituindo na fórmula P que encontramos. Deixamos o Ano constante e o cálculo da depreciação é a diferença do valor atual com o valor de 10000 a menos.
O que obtivemos foi
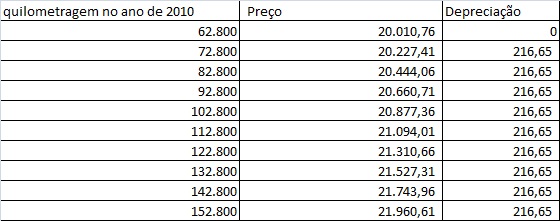
A depreciação é a mesma para todas as quilometragens.
Já para a depreciação anual, foi calculada da mesma maneira, porém mantendo-se uma quilometragem aleatória.
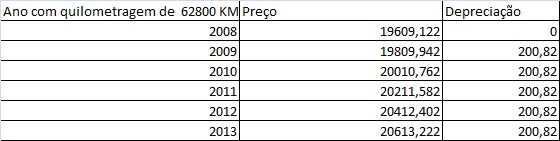
Bem como a da quilometragem, a depreciação anual também é a mesma, se mantém constante para todos os anos calculados .
Portanto a depreciação para cada 10000km rodados é de R$216,65 e a depreciação anual para o valor do carro é de R$200,82.
Como dito no enunciado, o Celta de Ana é de 2011 com 63000km rodados. Então, com a função encontrada na letra c, é possível encontrar qual o valor justo para o arro de Ana:
P=-384998,3144+200,8283462*A+0,021665991*K
**Substituindo
P=-384998,3144+200,8283462*2011+0,021665991*63000
O preço justo para o carro de Ana é P=R$20232,44
Sabemos que um polinômio de grau no máximo 2 é :
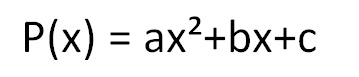
Então para encontrar o polinômio que satisfaça as condições, temos que fazer as devidas substituições em P(X).
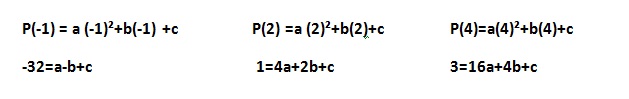
Feito isso, observamos que temos 3 equações com 3 incógnitas. Com o conhecimento da atividade anterior, sabemos que podemos trabalhar com essas equações atráves de sistemas lineares. Então escrevemos o nosso sistema
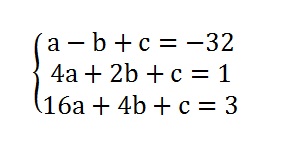
Para resolver esse sistema, vamos utilizar o método de eliminação de Gauss, que foi explicado na atividade 3.
Então vamos começar o nosso método multiplicando a segunda linha do nosso sistema por (-4) e somando com a terceira linha:
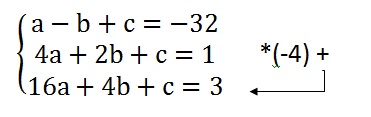
O novo sistema é:
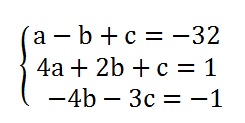
Agora, com esse novo sistema, multiplicamos a primeira linha por (-4) e somamos com a segunda linha do sistema:
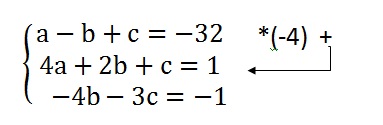
Obtemos então um outro novo sistema:
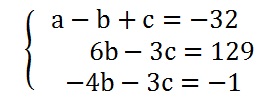
Mas ainda queremos deixar a terceira linha do sistema dependendo apenas de uma varíavel. Então multiplicamos a segunda linha por 2/3 e somamos com a terceira:
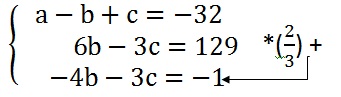
O novo sistema é :
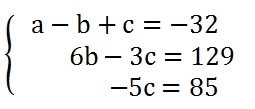
Com esse novo sistema, já podemos calcular quais os valores de cada variável

Dessa maneira, o polinômio P que satisfaz todas as condições impostas é:
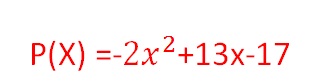
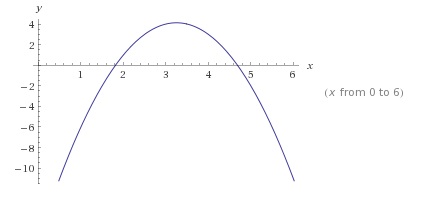
E o gráfico correspondente é uma parábola e por ele é possível determinar os zeros dessa equação, que são em x=1,8 e x=4,6.
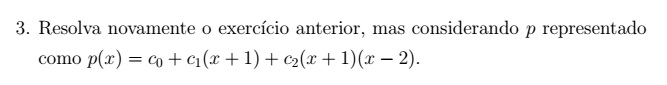
Começamos o exercício, substituindo os valores no polinômio dado no exercício:
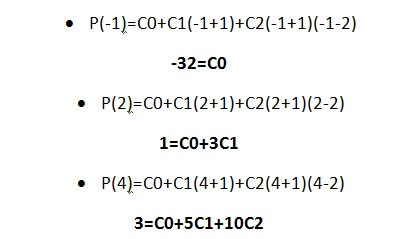
Seguindo o que foi feito no exercício 2, montamos um sistema linear com as equações que temos
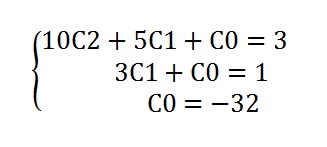
O que difere esse sistema do sistema do exercício anterior é que não precisamos aplicar nenhum método para resolvê-lo, somente substituimos:
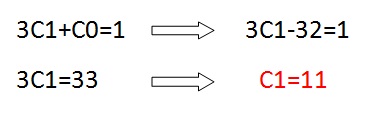
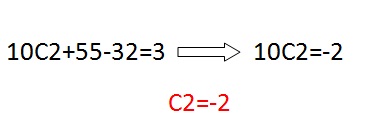
E C0=-32.
Dessa maneira, o polinômio que satisfaz as condições é :
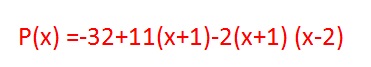
O gráfico desse polinômio está na imagem abaixo, com raízes em x=1,8 e x=4,6(aproximadamente) .
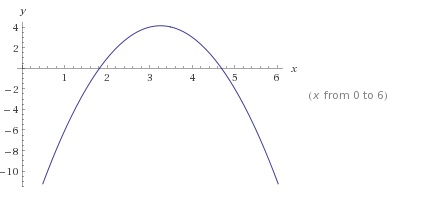

Para resolver esse exercício vamos utilizar a interpolação de Lagrange e antes de iniciarmos a resolução, vamos explicar como funciona esse método.
Interpolação, como dito no começo da atividade, é o que relaciona equações com valores tabelados.
Também foi dito que a interpolação pode não ser muito boa quando utilizada para fazer extrapolações, o que não impede dela ser usada para o mesmo.
Então para que se possa fazer extrapolações, aproxima-se uma função desconhecida por outra função. As funções desconhecidas mais utilizadas são os polinômios, isso porque eles têm integrais e derivadas simples de resolver e é sempre possível aproximar uma função contínua por um polinômio. Por isso para esse exercício vamos utilizar a interpolação polinomial de Lagrange
A interpolação polinomial de Lagrange garante que:
"Para (n+1) conjunto de dados {Xi,Yi} com i=0,1,2,...,n, para distintos Xi, existe UM único polinômio de grau menor ou igual a n, chamado de polinômio interpolador Pn(Xi)=Yi"
Esse polinômio interpolador é dado por :
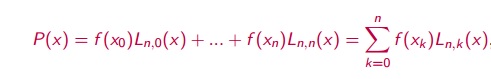
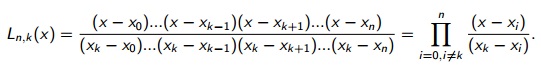
Vamos fazer um exemplo para melhor entendimento.
EXEMPLO
Associar f(x)=(1/x) por P(x) nos pontos x0=2, xi=2,5 e x2=4
Primeiro temos que definir Lo(x), L1(x) e L2(x).
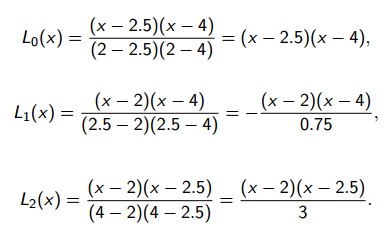
Como
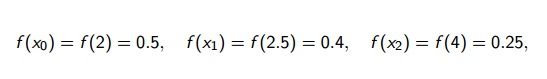
Então:
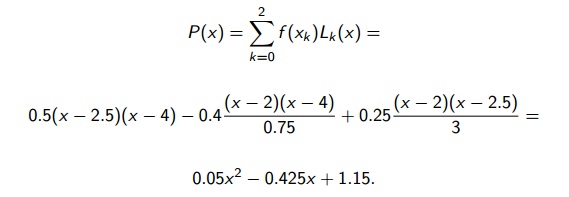
Vamos então resolver o nosso exercício.
Sabemos que o polinômio interpolador será:
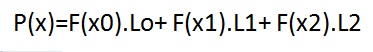
Calculamos então L0, L1 e L2 e os respectivos valores das funções.
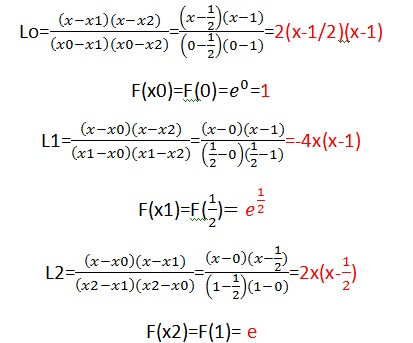
O polinômio interpolador é :
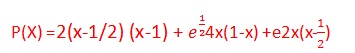
Plotando o gráfico da função f(x) (representado pela curva na cor vermelha) e do polinômio de interpolação (representado pela curva na cor azul)
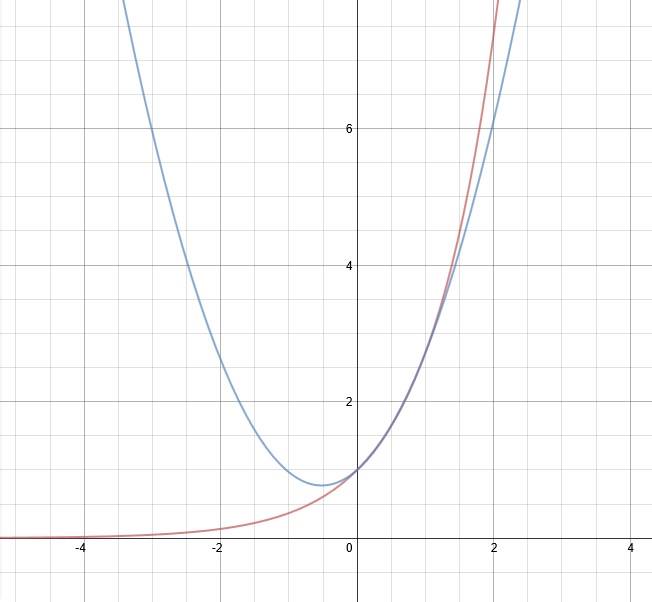
Como a diferença é muito pequena, demos dois zooms em duas regiões do gráfico, o primeiro de [0, 0.4] e o segundo [0.55, 1]. De [0.4, 0.55] está o 0,5 que é o ponto de interpolação, com certeza não era o pior ponto, por isso não colocamos esse intervalo.
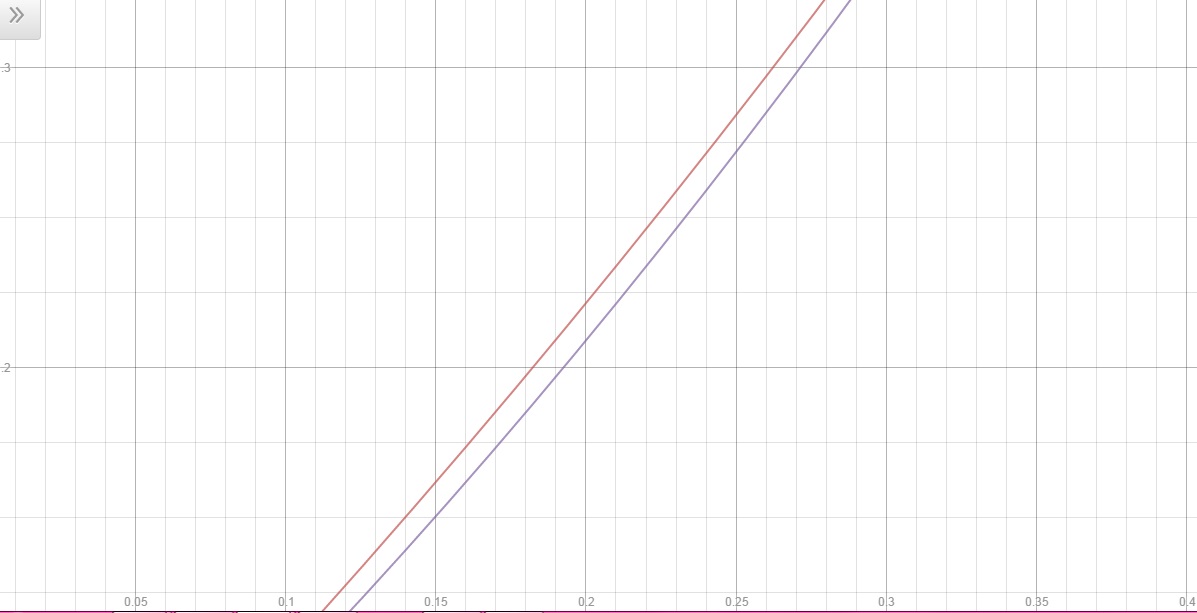
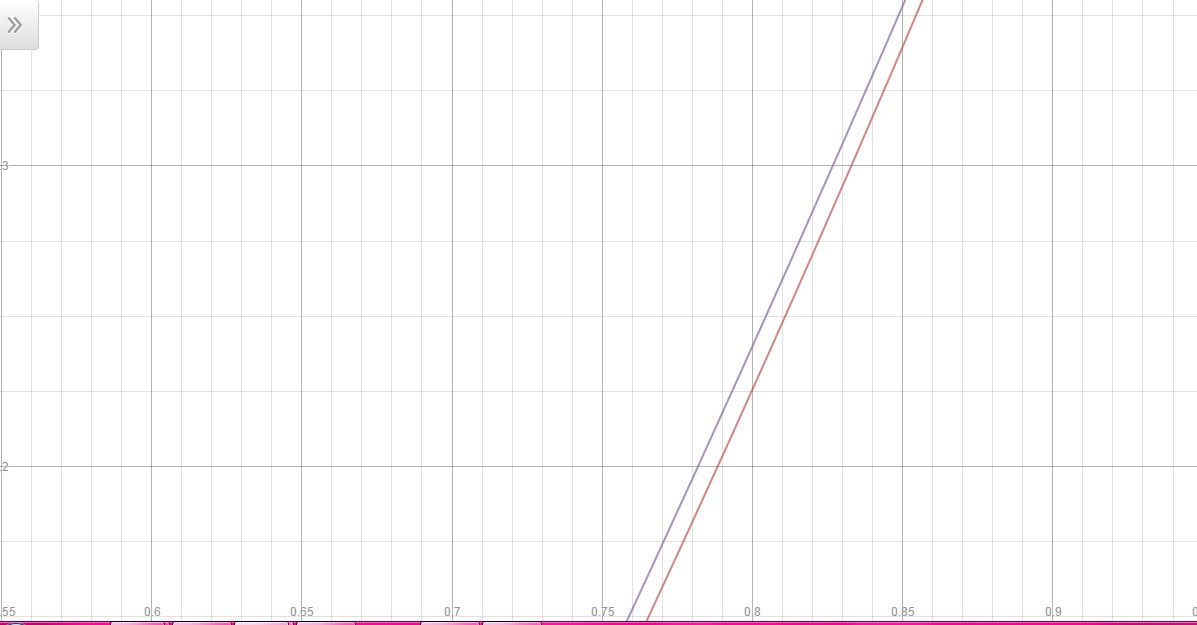
Comparando as duas imagens, aparentemente é muito difícil concluir qual possui uma aproximação pior.
Uma imagem mais geral nos ajuda um pouco com a determinação
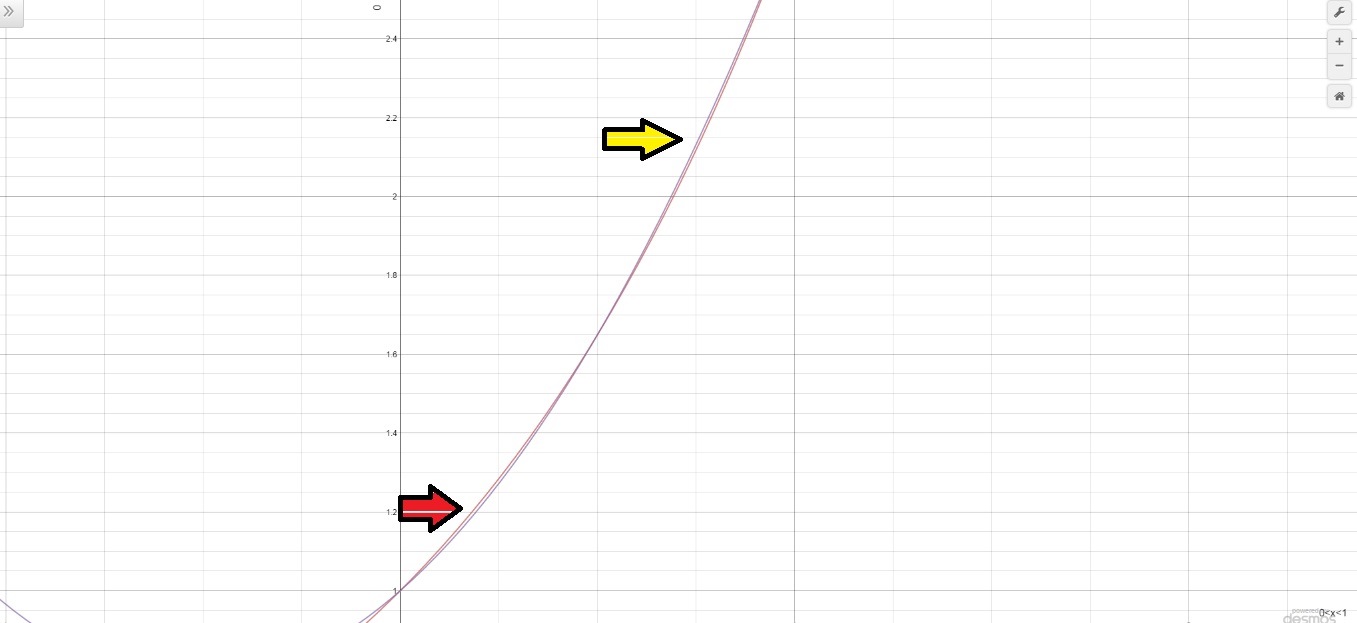
Com essa última imagem, ficou um pouco mais fácil saber qual foi o pior intervalo, então podemos concluir que o ponto com pior arpoximação está no intervalo de [0,0.4]. E aparentemento esse ponto é 0,25. No Segundo intervalo considerado [0.55, 1] tem-se uma ruim aproximação em 0,75 mais ou menos. Agora comparando as aproximações em 0,25 e 0,75 não é possível concluir qual deles é a pior.

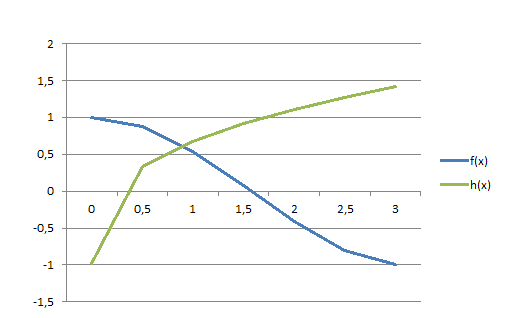
Primeiro plotamos o gráfico das duas funções juntas para termos uma ideia de como g(x) se comporta.
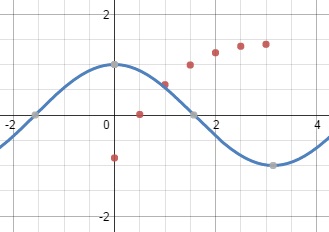
Vamos ajustá-las para a forma h(x)=a*x^(1/3)+ b.
Vamos usar A*X=B, onde A é a matriz:
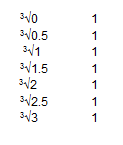

Multiplicamos os dois lados da equação pela transposta de A:
At * A * X = At * B
X= (At * A)^-1* At * B

Já resolvendo as raízes:
At * A= 8.4498 6.9978
6.9978 7
At * B= 7.1618
4.745
A matriz inversa de (At * A) foi encontrada pelo método de eliminação de Gauss-Jordan.
(At *A)^-1 = 0.6875 -0.6874
-0.6874 0.83
(At * A)^-1 * (At * B) = 1.6620
-0.9846
Logo, a = 1.6620 e b= -0.9846
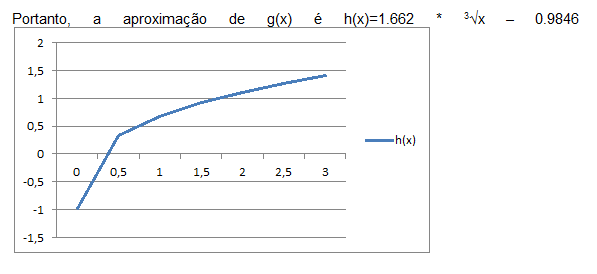
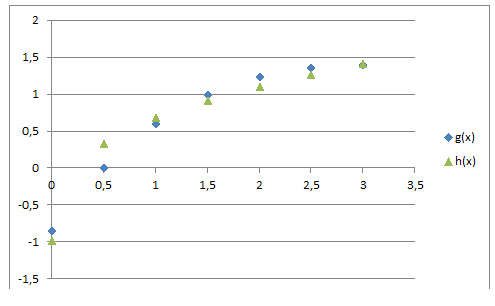
Vamos igualar as funções para descobrir o valor aproximado do ponto de interseção x':
f(x)=h(x)
cos (x) = 1.662 * 3√x - 0.9846
x'≈0.9011