Lista 5

Integração numérica

A ideia básica desse método de integração numérica é substituir f(x) por um polinômio que a aproxime no intervalo [a, b]. Então o problema fica resolvido pela integração de polinômios. 

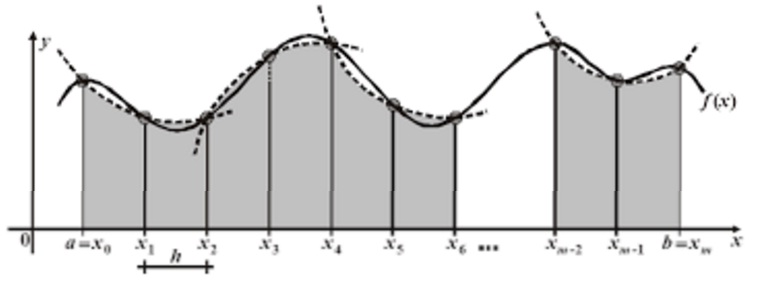
Para resolver esses problemas vamos utilizar as Fórmulas de Newton-Cotes.

Fórmulas de Newton-Cotes

As fórmulas de Newton-Cotes são um conjunto de fórmulas para integração numérica. Essas fórmulas podem ser úteis se o valor da integral, em pontos igualmente espaçados, está disponibilizado.

Então primeiro assume-se que o valor da função f, definida entre [a,b] é conhecido em pontos Xi igualmente espaçados, onde x0=a e xn=b.

Há dois tipos de Fórmulas de Newton-Cotes :

• Fechadas: Utilizam o valor da função em todos os pontos;

• Abertas: Não utilizam os valores da função nas extremidades;

As fórmulas fechadas de Newton-Cotes são fórmulas de integração do tipo:

Sendo que os coeficientes são determinados de acordo com o grau do polinômio aproximado.

Dentro do conjunto das Fórmulas de Newton-Cotes Fechadas, temos a regra do trapézio e a regra de Simpson.

Regra do trapézio

O objetivo da regra do trapézio é aproximar a função que se tem, f(x), por um polinômio de grau 1.

Quando se aproxima a função por uma reta, a área do gráfico pode ser aproximada pela área de um trapézio. 

Para encontrar o polinômio de ordem 1, podemos usar Lagrange, que já foi explicado na última atividade de ajuste de curvas.

O polinômio de ordem 1 então será:

Se chamarmos na nossa altura h como h=(x1-x0)/n , onde n é o número de subdivisões do intervalo, como nesse caso o n=1, podemos escrever nosso polinômio como: 

Agora que já temos a nossa aproximação, a integral da função f(x) pode ser escrita como: 

Então a integral de f(x) no intervalo [a,b] pode ser aproximada pela área de um trapézio de base menor f(x0) e base maior f(x1) e altura h.

Mas essa aproximação, como pode ser visto graficamente, não é muito boa. Mas se aplicarmos essa regra do trapézio várias vezes, a aproximação vai ser cada vez melhor. 

Regra do Trapézio repetida

O objetivo aqui é repetir a regra do trapézio para obter uma melhor aproximação. Então tem-se o intervalo [a,b] e dividindo-o em subintervalos de larguras iguais h=(b-a)/n, onde n é o número de subdivisões dentro do intervalo.

Então a integral de f(x) pode ser escrita como sendo a soma de todos os trapézios que estão no intervalo.

Portanto a aproximação para a integral é 

Já vimos a regra dos trapézios agora vamos explicar mais sobre a outra fórmula de Newton-Cote fechada: Regra de Simpson.

Regra de Simpson

Na regra de Simpson, ao invés de aproximar f(x) por um polinômio interpolador de grau 1, aproxima-se por um polinômio interpolador de grau 2.

Para que possamos aproximar por uma parábola, vamos precisar de mais um ponto. Esse ponto é o ponto médio.

Então escrevendo nosso polinômio interpolador, temos:

Sabemos também que 

O nosso polinômio interpolador é 

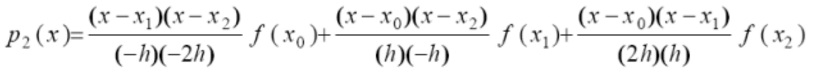
A integral pode ser escrita como: 

Bem como a regra dos trapézios simples, essa aproximação também é um pouco grosseira e por isso, há a regra de Simpson Repetida.

Regra de Simpson Repetida

Ou também conhecida como Regra ⅜ de Simpson, serve para encontrarmos uma melhor aproximação.

Para isso, repetimos o procedimento que fizemos na regra dos trapézios repetida: Dividimos o nosso intervalo [a,b] em n pares de subintervalos.

O número de subintervalos é representado aqui no nosso caso pela letra M=2n.

Então aplicamos a regra de Simpson simples para cada um dos subintervalos M e a integral pode ser escrita como

Onde f(x0) e f(xm ) são os valores da função nas extremidades; O termo seguinte é a somatória do valor da função em subintervalos de índices pares, excluindo as extremidades e o ultimo termo é a somatória do valor da função nos subintervalos de índices impares.

Agora que já possuímos o embasamento teórico, podemos resolver as questões propostas.

Pela regra dos trapézios:

Como temos os subintervalos e sabemos pela explicação acima que a regra dos trapézios repetida nos fornece uma aproximação melhor, vamos fazer então por essa maneira.

Vamos dividir o subintervalos em uma separação de 0,25 (que é o que está indicado na tabela). Já vimos a cima que o modo para calcular a aproximação da integral é dada por:

Para que possamos ter uma separação de 0,25, é preciso dividir o intervalo em 4 subdivisões. Pela tabela, nós já temos os valores de cada subdivisão então agora basta calcular. 

O resultado obtido foi 0,063302125; 

O resultado obtido pela regra dos trapézios simples foi o dobro da obtida pela regra dos trapézios repetida. 

Pela Regra de Simpson:

Usaremos também aqui a regra de Simpson Repetida.

Então, como já foi explicado anteriormente, para calcular temos que substituir os valores na seguinte relação:

Sabemos que o valor do intervalo é de 0,25;

Substituindo temos que: 

E o resultado obtido foi 0,06200858333333.....

Comparando os dois resultados é possível concluir que os dois métodos forneceram valores muito próximos entre si. O erro será calculado na questão C.

Vamos fazer a mesma coisa que fizemos para o item anterior porém o limite superior foi modificado.

Regra dos Trapézios:

Substituindo na expressão dada na explicação e também escrita na letra a temos que a nossa aproximação é: 

O valor obtido foi de 0,0661711875; 

Regra de Simpson:

Assim como feito na letra a, substituímos nossos valores na expressão dada na explicação (e que também está na letra a) e obtemos: 

O valor que essa expressão nos fornece é 0,06392129166666....

Comparando os valores dos dois métodos, tivemos valores próximos. 

O erro relativo é calculado como 

Onde p é o número exato, que o enunciado do exercício nos forneceu e p* é o número que chegamos pelas nossas contas.

Então vamos calcular o erro relativo para A.

Pela regra dos trapézios, o valor obtido foi de 0,063302125

Então o erro relativo é

Já pela regra de Simpson, o valor encontrado foi 0,06200858333333

Então o erro é relativo é 

Vamos calcular o erro relativo para B.

Pela regra dos trapézios, o valor obtido foi de 0,0661711875

Então o erro relativo é 

Pela regra de Simpson o valor para B encontrado foi de 0,06392129166666....

O erro absoluto é de : 

Podemos concluir que em ambas integrais, o erro foi menor quando calculadas pela regra de Simpson. Na integral A, a diferença de erro entre as duas regras foi de 0,02086 enquanto que na integral B essa diferença foi bem menor, 0,008774442.

Baseado nos erros relativos das duas integrais é possível afirmar que há uma melhor aproximação ao valor real da integral quando usa-se um polinômio interpolador de grau 2, ou seja, quando usa-se a regra de Simpson. 

A estimativa de erro para a regra de Simpson repetida( pois vamos descobrir a quantidade de subintervalos) é dada pela fórmula abaixo : 

Onde f4(x) é a derivada quarta de f(x).

Mas se lembrarmos que 

Vamos obter então 

Podemos calcular n (e consequentemente calcular m) com a seguinte relação: 

Onde

Então com isso, vamos o valor mínimos de subintervalos para que possamos ter o erro pedido. Depois disso, vamos calcular o valor da integral por aproximação, usando a regra de Simpson.

Já foi dado no exercício que Ers=10^-3.

Então temos que calcular Es.

Valor de b=2

Valor de a=1

O valor máximo para essa derivada no intervalo [1,2] é quando x=1 e a resposta é -6, mas como está em módulo, então usamos 6. 

Sabemos que 

Já temos todos os valores que precisamos para calcular N, agora basta substituí-los. 

N tem que ser um número inteiro, portanto n=2. Mas n é o número de pares de subintervalos, portanto o número de subintervalos mínimo para obter o erro de 10^-3 é 2xn=2x2=4.

Agora que nós já temos a quantidade de subintervalos, basta aplicar a regra de Simpson. Então vamos montar uma tabela com os valores de x e f(x) num intervalo de h=(2-1)/4=0,25.

Então substituindo da regra de Simpson repetida temos: 

E o resultado obtido 4,13609558333....

Calculamos a integral dada no enunciado no wolfram e obtivemos o seguinte resultado:

Portanto podemos ver que o erro está dentro do especificado no enunciado.

Para resolver esse exercício vamos utilizar a mesma lógica do exercício anterior.

Vamos começar então com com F1(x).

Então sabemos que o erro das integrais pode ser calculado como 

Esr já foi dado pelo exercício= 10^-4

O limite superior b=5

O limite inferior a=0

Calculado no wolfram a derivada quarta de f1(x): 

Essa derivada tem valor máximo em x=3 quando é igual a 17,4190394482.

 Sabemos do exercício anterior que 

Substituindo os valores: 

Então o valor de n é: 

Como dito no item anterior, n tem que ser um valor inteiro, então n=21. Mas n é o número de pares de subintervalos, então deve haver 21*2=42; 42 subintervalos para que o erro seja menor que 10^-4. 

Agora para f2(x):

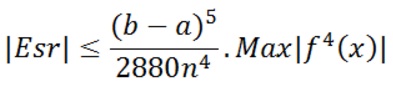
O Esr é o mesmo do anterior=10^-4

Limite inferior=0

Limite superior=π

Foi calculado no wolfram a derivada quarta de f2(x):

O máximo dessa derivada ocorre em π que vale 92,56277053111707

Então N vale: 

Como já dito anteriormente, n tem que ser um número inteiro, então n=18. O número de subintervalos é 2xn. Então o número mínimo de subdivisões é 36. 

Vamos primeiramente resolver usando a regra dos trapézios. 

O intervalo dado é h=0,2.

F(xo)=3,12014

F(xm)=10,46675 

O resultado é 4,399681. 

Agora pelo método de Simpson temos que 

Substituindo os valores, obtemos a expressão:

O resultado obtido foi 4,154794.

A diferença de valores entre os dois métodos foi de 0,244887.

Sabemos que os valores dados de f(x) nesse exercício são os erros dos valores de f(x) do exercício anterior. Portanto, para descobrirmos qual o erro associado a cada método, vamos somar o erro de f(x) ao valor de f(x) e então calcular a diferença entre as integrais.

Pelo método dos trapézios, utilizamos a fórmula dada na explicação, e que também foi utilizada no exercício 4 , e subtituimos os valores e o que obtivemos foi:

E o resultado foi 4,39968064.

O resultado dessa integral sem os erros associados, obtido no exercicio 4, é 4,399681. O erro desse método é: 3,6x10^-7.

Agora pelo método de simpson, usamos também a mesma fórmula do exercício 4, substituimos os valores e obtivemos:

O resultado obtido foi 4,154793373.

O erro desse método é 6,267x10^-7.

Portanto, o erro dos dois métodos é muito pequeno, isso acontece porque o erro associado a f(x) é um erro muito pequeno, na ordem de 10^-6.